Giải bài 2.25 trang 44 SGK Toán 8 tập 1 - Kết nối tri thức
Một mảnh vườn hình vuông có độ dài cạnh bằng x (mét).
Đề bài
Một mảnh vườn hình vuông có độ dài cạnh bằng x (mét). Người ta làm đường đi xung quanh mảnh vườn, có độ rộng như nhau và bằng y (mét) (H.2.2)
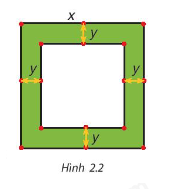
a) Viết biểu thức tính diện tích S của đường bao quanh mảnh vườn theo x và y.
b) Phân tích S thành nhân tử rồi tính A khi x=102 m, y=2 m.
Phương pháp giải - Xem chi tiết
Viết biểu thức.
Diện tích đường bao quanh = diện tích mảnh vườn hình vuông – diện tích bên trong vườn.
Phân tích đa thức thành nhân tử.
Lời giải chi tiết
a) \(S = {x^2} - {\left( {x - 2y} \right)^2}\)
b) \(S = {x^2} - {\left( {x - 2y} \right)^2}\)
\(= \left( {x - x + 2y} \right)\left( {x + x - 2y} \right)\)
\(= 2y.\left( {2x - 2y} \right) \)
\(= 2y.2\left( {x - y} \right) = 4y\left( {x - y} \right)\)
Khi x = 102 m, y = 2 m thì \(S = 4.2.\left( {102 - 2} \right) = 800 ({m^2})\)