Giải bài 2. 3 trang 18 sách bài tập toán 10 - Kết nối tri thức với cuộc sống — Không quảng cáo

Đề bài

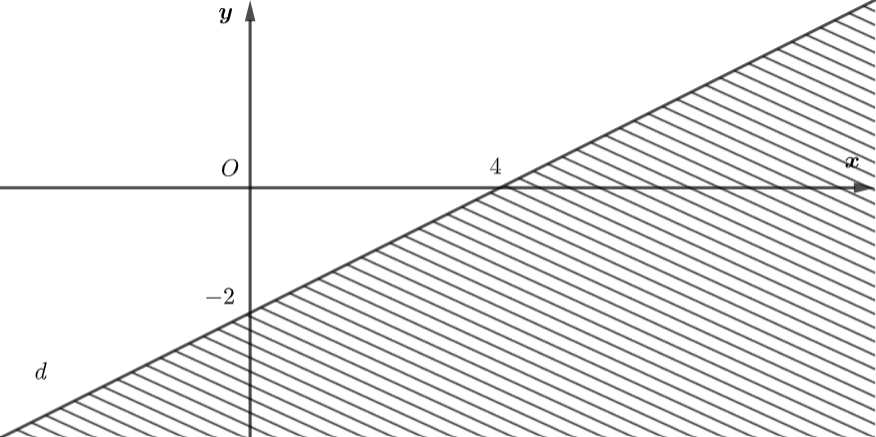
Xác định một bất phương trình bậc nhất hai ẩn nhân nửa mặt phẳng bờ là đường thẳng \(d\)  (miền không bị gạch) làm miền nghiệm.

Lời giải chi tiết

Gọi đường thẳng \(d\) cần tìm là: \(d:y = ax + b,\,\,\left( {a \ne 0} \right).\)

Nhìn vào độ thị thì đường thẳng \(d\) đi qua điểm \(A\left( {4;0} \right)\) và \(B\left( {0; - 2} \right)\)

Thay điểm \(A\left( {4;0} \right)\) vào \(d\) ta được: \(4a + b = 0.\)

Thay điểm \(B\left( {0; - 2} \right)\) vào \(d\) ta được: \(0a + b =  - 2\,\, \Rightarrow \,\,b =  - 2\)

Ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{c}}{4a + b = 0}\\{b =  - 2}\end{array}} \right.\,\, \Rightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{a = \frac{1}{2}}\\{b =  - 2}\end{array}} \right.\)

\( \Rightarrow \,\,d:y = \frac{1}{2}x - 2\,\, \Leftrightarrow \,\,x - 2y = 4.\)

Vì miền nghiệm của đồ thị là nửa mặt phẳng bờ \(d\) chứa điểm \(O\) nên bất phương trình cần tìm là: \(x - 2y \le 4\)