Giải bài 2 trang 108 SGK Toán 8 tập 1 - Cánh diều
Cho tam giác ABC có
Đề bài
Cho tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G. Gọi P và Q lần lượt là trung điểm của GB và GC. Chứng minh tứ giác PQMN là hình bình hành.
Phương pháp giải - Xem chi tiết
Chứng minh tứ giác PQMN có hai đường chéo cắt nhau tại trung điểm của mỗi đường
Lời giải chi tiết
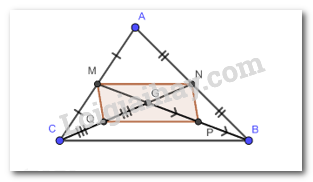
\(\Delta ABC\) có hai đường trung tuyến BM và CN cắt nhau tại G.
Suy ra G là trọng tâm của tam giác.
\( \Rightarrow BG = \dfrac{2}{3}BM;GM = \dfrac{1}{3}BM\left( 1 \right)\)
Mà: \(PG = \dfrac{1}{2}BG = \dfrac{1}{2}.\dfrac{2}{3}BM = \dfrac{1}{3}BM\left( 2 \right)\)
Từ (1), (2) suy ra GM = PG
Chứng minh tương tự ta cũng có QG = GN
Tứ giác PQMN có hai đường chéo QN và PM cắt nhau tại trung điểm mỗi đường nên tứ giác PQMN là hình bình hành