Giải bài 2 trang 119, 120 vở thực hành Toán 9 — Không quảng cáo

Đề bài

Khi chuyển động, giả sử đầu mũi kim dài của một chiếc đồng hồ vạch nên một đường tròn, kí hiệu là (T1), trong khi đầu mũi kim ngắn vạch nên một đường tròn khác, kí hiệu là (T2).

a) Hai đường tròn (T1) và (T2) có vị trí tương đối như thế nào?

b) Giả sử bán kính của (T1) và (T2) lần lượt là ${R_1}$ và ${R_2}$. Người ta vẽ trên mặt đồng hồ một họa tiết hình tròn có tâm nằm cách điểm trục kim đồng hồ một khoảng bằng $\frac{1}{2}{R_1}$ và có bán kính bằng $\frac{1}{2}{R_2}$. Hãy cho biết vị trí tương đối của đường tròn (T3) đối với mỗi đường tròn (T1) và (T2). Vẽ ba đường tròn đó nếu ${R_1} = 3cm$ và ${R_2} = 2cm$.

Lời giải chi tiết

(H.5.39)

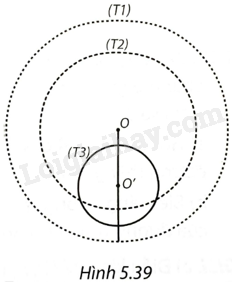
a) (T1) và (T2) là hai đường tròn đựng nhau, (T1) đựng (T2) với tâm O là điểm trục của hai kim đồng hồ.

b) (T2) là đường tròn tạo bởi đầu kim ngắn nên ${R_2} < {R_1}$ (1).

Gọi O’ là tâm và ${R_3}$ là bán kính của đường tròn (T3). Theo đề bài, ta có: ${R_3} = \frac{1}{2}{R_2}$ và $OO' = \frac{1}{2}{R_1}$ (2)

+ Xét hai đường tròn (T1) và (T3), tức là hai đường tròn $\left( {O;{R_1}} \right)$ và $\left( {O';\frac{1}{2}{R_2}} \right)$. Từ (1) và (2), ta có: ${R_1} - {R_3} = {R_1} - \frac{1}{2}{R_2} = \frac{1}{2}\left( {{R_1} - {R_2}} \right) + \frac{1}{2}{R_1} > \frac{1}{2}{R_1}$, suy ra ${R_1} - {R_3} > OO'$.

Do đó, (T1) đựng (T3).

+ Xét hai đường tròn (T2) và (T3), tức là hai đường tròn $\left( {O;{R_2}} \right)$ và $\left( {O';\frac{1}{2}{R_2}} \right)$. Từ (2) ta có: ${R_2} - {R_3} = {R_2} - \frac{1}{2}{R_2} = \frac{1}{2}{R_2} > 0$ (3)

Mặt khác, ${R_2} + {R_3} = {R_2} + \frac{1}{2}{R_2} = \frac{3}{2}{R_2}$. Do đó:

- Nếu $3{R_2} > {R_1}$ thì ${R_2} + {R_3} = \frac{3}{2}{R_2} > \frac{1}{2}{R_1} = OO'$, tức là ${R_2} + {R_3} > OO'$. Kết hợp với (3) ta thấy (T2) và (T3) cắt nhau.

- Nếu $3{R_2} = {R_1}$ thì ${R_2} + {R_3} = \frac{3}{2}{R_2} = \frac{1}{2}{R_1} = OO'$, tức là ${R_2} + {R_3} = OO'$ và ta có (T2) và (T3) tiếp xúc với nhau.

- Nếu $3{R_2} < {R_1}$ thì ${R_2} + {R_3} = \frac{3}{2}{R_2} < \frac{1}{2}{R_1} = OO'$, tức là ${R_2} + {R_3} < OO'$ và ta có (T2) và (T3) ngoài nhau.