Giải bài 27 trang 32 SBT toán 10 - Cánh diều
a) Biểu diễn miền nghiệm của các bất phương trình sau: \(\left\{ {\begin{array}{*{20}{c}}{3x - y \le 9}\\{3x + 6y \le 30}\\{x \ge 0}\\{0 \le y \le 4}\end{array}} \right.\left( I \right)\)
Đề bài
a) Biểu diễn miền nghiệm của các bất phương trình sau: \(\left\{ {\begin{array}{*{20}{c}}{3x - y \le 9}\\{3x + 6y \le 30}\\{x \ge 0}\\{0 \le y \le 4}\end{array}} \right.\left( I \right)\)
b) Tìm x, y là nghiệm của hệ bất phương trình (I) sao cho \(F = 3x + 4y\) đạt giá trị lớn nhất
Phương pháp giải - Xem chi tiết
a) Xác định miền nghiệm của từng bpt. Miền nghiệm của hệ bpt là miền giao của các miền nghiệm ấy.
Biểu diễn miền nghiệm của bpt \(ax + by < c\)
Bước 1: Vẽ đường thẳng \(d:ax + by = c\)
Bước 2: Lấy một điểm \(M\left( {{x_o};{y_o}} \right)\) không thuộc d (ta thường lấy gốc tọa độ O nếu \(c \ne 0\)). Tính \(a{x_o} + b{y_o}\) và so sánh với c
Bước 3: Kết luận
Nếu \(a{x_o} + b{y_o} < c\)thì nửa mặt phẳng (không kể đường thẳng d) chứa điểm M là miền nghiệm của bất phương trình \(ax + by < c\)
Nếu \(a{x_o} + b{y_o} > c\) thì nửa mặt phẳng (không kể d) không chứa điểm M là miền nghiệm của bất phương trình \(ax + by > c\)
b) Tính giá trị của \(F\left( {x;y} \right)\) tại các đỉnh của miền đa giác nghiệm.
Lời giải chi tiết
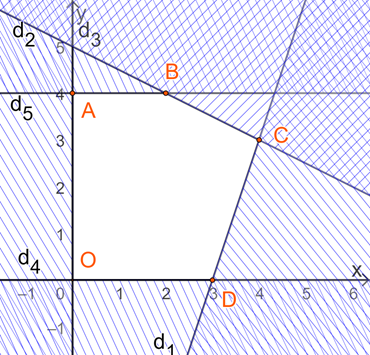
Vẽ các đường thẳng:
d1: 3x – y = 9 đi qua hai điểm có tọa độ là (3; 0) và (0; 9).
d2: 3x + 6y = 30 đi qua hai điểm (10; 0) và (0; 5).
d3: x = 0 là trục tung.
d4: y = 0 là trục hoành
d5: y = 4 đi qua điểm (0; 4) và song song với trục hoành.
Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.
Miền nghiệm của hệ bất phương trình là miền ngũ giác OABCD với O(0; 0), A(0; 4), B(2; 4), C(4; 3), D(3; 0):
b) Thay x,y lần lượt là tọa độ các điểm O, A, B, C, D vào biểu thức F:
|
\(O(0;0)\) |
\(A(0;4)\) |
\(B(2;4)\) |
\(C(4;3)\) |
\(D(3;0)\) |
|
|
\(F = 3x + 4y\) |
\(0\) |
\(16\) |
\(22\) |
\(24\) |
\(9\) |
F đạt giá trị lớn nhất bằng 24 tại \(x = 4,y = 3\)