Giải bài 29 trang 100 sách bài tập toán 11 - Cánh diều — Không quảng cáo

Đề bài

Cho hình chóp $S.ABCD$ có $SA \bot \left( {ABCD} \right)$, $ABCD$ là hình thoi cạnh $a$, $AC = a$, $SA = \frac{a}{2}$. Tính số đo của góc nhị diện $\left[ {S,CD,A} \right]$.

Lời giải chi tiết

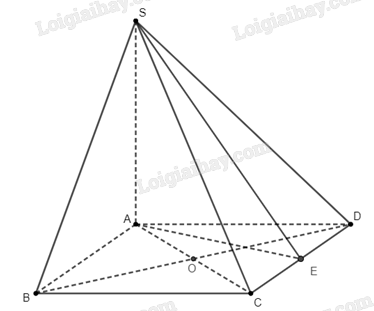
Gọi $E$ là hình chiếu của $A$ trên $CD$. Do $SA \bot \left( {ABCD} \right)$ nên ta suy ra $SA \bot CD$. Do $AE \bot CD$ nên ta suy ra $\left( {SAE} \right) \bot CD$, điều này dẫn tới $SE \bot CD$.

Như vậy do $SE \bot CD$, $AE \bot CD$ nên góc $\widehat {SEA}$ là góc phẳng nhị diện của góc nhị diện $\left[ {S,CD,A} \right]$.

Tam giác $ACD$ đều ($AC = CD = AD = a$) nên ta suy ra $AE = \frac{{a\sqrt 3 }}{2}$.

Xét tam giác $SAE$ vuông tại $A$, ta có $\tan \widehat {SEA} = \frac{{SA}}{{AE}} = \frac{{\frac{a}{2}}}{{\frac{{a\sqrt 3 }}{2}}} = \frac{{\sqrt 3 }}{3}$.

Vậy $\widehat {SEA} = {30^o}$.