Giải bài 29 trang 73 SBT toán 10 - Cánh diều
Cho tam giác ABC, biết toạ độ trung điểm các cạnh BC, CA, AB lần lượt là M(-1 ; 1), N(3 ; 4), P(5 ; 6).
Đề bài
Cho tam giác ABC , biết toạ độ trung điểm các cạnh BC , CA , AB lần lượt là M (-1 ; 1), N (3 ; 4), P (5 ; 6).
a) Viết phương trình tham số của các đường thẳng AB , BC , CA
b) Viết phương trình tổng quát của các đường trung trực của tam giác ABC
Phương pháp giải - Xem chi tiết
Bước 1: Tìm tọa độ các vectơ \(\overrightarrow {MN} ,\overrightarrow {MP} ,\overrightarrow {NP} \) rồi xác định các VTCP của AB , BC , CA
Bước 2: Viết PT tham số của các đường thẳng AB , BC , CA khi biết điểm đi qua và VTCP
Bước 3: Tìm các VTPT của các đường trung trực của ∆ ABC là các vectơ \(\overrightarrow {MN} ,\overrightarrow {MP} ,\overrightarrow {NP} \)
Bước 4: Viết PTTQ các đường trung trực của tam giác ABC
Lời giải chi tiết
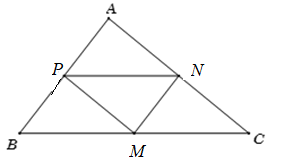
a) Theo giả thiết, MN , MP , NP là các đường trung bình của ∆ ABC \( \Rightarrow MN//AB,MP//AC,NP//BC\)
Khi đó, AB , AC , BC lần lượt nhận các vectơ \(\overrightarrow {MN} = (4;3),\overrightarrow {MP} = (6;5),\overrightarrow {NP} = (2;2)\) làm VTCP
+ AB đi qua P , nhận \(\overrightarrow {MN} = (4;3)\) làm VTCP nên có PT tham số: \(\left\{ \begin{array}{l}x = 5 + 4t\\y = 6 + 3t\end{array} \right.\)
+ AC đi qua N , nhận \(\overrightarrow {MP} = (6;5)\) làm VTCP nên có PT tham số: \(\left\{ \begin{array}{l}x = 3 + 6k\\y = 4 + 5k\end{array} \right.\)
+ BC đi qua M , nhận \(\overrightarrow u = (1;1)\)cùng phương với \(\overrightarrow {NP} = (2;2)\) làm VTCP nên có PT tham số:
\(\left\{ \begin{array}{l}x = - 1 + p\\y = 1 + p\end{array} \right.\)
b) Ta có:
+ Đường trung trực của cạnh AB đi qua P và nhận \(\overrightarrow {MN} = (4;3)\) làm VTPT nên có PTTQ:
4 x + 3 y – 38 = 0
+ Đường trung trực của cạnh AC đi qua N và nhận \(\overrightarrow {MP} = (6;5)\) làm VTPT nên có PTTQ:
6 x + 5 y – 38 = 0
+ Đường trung trực của cạnh BC đi qua M và nhận \(\overrightarrow {NP} = (2;2)\) làm VTPT nên có PTTQ:
2 x + 2 y = 0 \( \Leftrightarrow x + y = 0\)