Giải bài 3.23 trang 75 SGK Toán 8 - Cùng khám phá
Giải thích vì sao các tứ giác trong hình 3.63 là hình chữ nhật.
Đề bài
Giải thích vì sao các tứ giác trong hình 3.63 là hình chữ nhật.
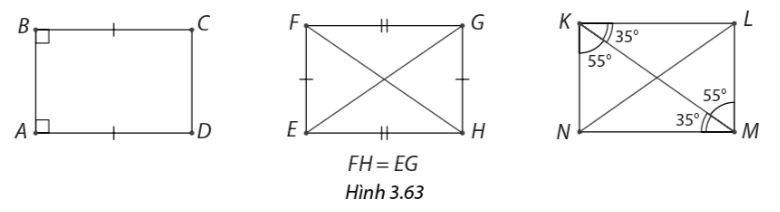
Phương pháp giải - Xem chi tiết
Sử dụng dhnb hình chữ nhật:
Hình bình hành có một góc vuông là hình chữ nhật.
Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
Lời giải chi tiết
Xét tứ giác ABCD có:
\(BC \bot AB;AD \bot AB \Rightarrow BC//AD\) và \(BC = AD\) suy ra ABCD là hình bình hành (dhnb)
Mà \(\widehat A = 90^\circ \) suy ra ABCD là hình chữ nhật (dhnb).
Xét tứ giác EFGH có:
\(FG = EH;EF = GH\) suy ra EFGH là hình bình hành (dhnb)
Mà \(FH = EG\) suy ra EFGH là hình chữ nhật (dhnb).
Xét tứ giác \(KLMN\) có \(\widehat {LKM} = \widehat {KMN};\widehat {NKM} = \widehat {KMN}\) mà các góc nằm ở vị trí so le trong nên suy ra \(KL//MN;KN//LM.\) Vậy KLMN là hình bình hành (dhnb).
Mà có \(\widehat K = 55^\circ + 35^\circ = 90^\circ \) nên KLMN là hình chữ nhật (dhnb).