Giải bài 3.44 trang 90 SGK Toán 8 - Cùng khám phá
Chứng minh rằng:
Đề bài
Chứng minh rằng:
a) Trong một hình bình hành (không là hình thoi), các tia phân giác của các góc cắt nhau tạo thành một hình chữ nhật.
b) Trong một hình chữ nhật (không là hình vuông), các tia phân giác của các góc cắt nhau tạo thành một hình vuông.
Phương pháp giải - Xem chi tiết
Dựa vào tính chất hình bình hành, hình chữ nhật hình vuông để chứng minh.
Lời giải chi tiết
a) Ta có hình bình hành \(ABCD\):
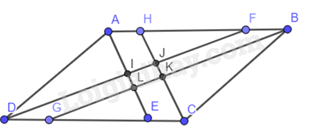
Ta có \(\widehat {EAB} = \widehat {AED}\) ( sole trong)
Lại có \(\widehat {EAB} = \widehat {HCD}\) (đường phân giác của hai góc đối trong hình bình hành)
→ \(\widehat {AED} = \widehat {HCD}\)
→ \(AE//HC\)
→ \(IL//JK\) (1)
Có \(\widehat {FDC} = \widehat {ABG}\) (đường phân giác của hai góc đối trong hình bình hành)
Mà \(\widehat {ABG} = \widehat {BGC}\) (sole trong)
→ \(DF//BG\)
→ \(IJ//LK\) (2)
Từ (1) và (2) suy ra \(IJKL\) là hình bình hành
Ta có \(\widehat {AED} = \widehat {EAB}\)
Mà \(\widehat {EAB} + \widehat {CDF} = 90^\circ \) (phân giác của hai góc kề trong hình bình hành)
→ \(\widehat {AED} = \widehat {CDF} = 90^\circ \)
→ \(\widehat {DIE} = 90^\circ \)
→ \(\widehat {JIL} = 90^\circ \)
→ \(IJKL\) là hình chữ nhật.
b) Cho hình chữ nhật \(ABCD\):
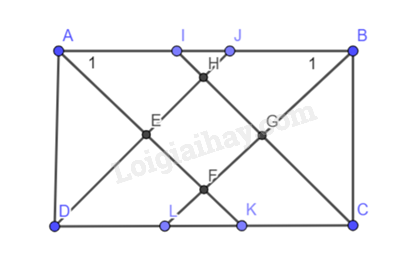
\(ABCD\) là hình chữ nhật \( = > \widehat A = \widehat B = 90^\circ \)
\(AF,BF\) lần lượt là phân giác của \(\widehat A,\widehat B = > \widehat {BAF} = \widehat {ABF} = \frac{1}{2}\widehat A = \frac{1}{2}\widehat B = \frac{1}{2}90^\circ = 45^\circ \)
Xét tam giác \(ABF\) có: \(\widehat {BAF} + \widehat {ABF} + \widehat {AFB} = 180^\circ \)
\(\begin{array}{l}2\widehat {BAF} + \widehat {AFB} = 180^\circ \\ = > \widehat {AFB} = 180^\circ - 2\widehat {BAF} = 180^\circ - 2.45^\circ = 90^\circ \end{array}\)
Chứng minh tương tự, ta có \(\widehat {DHC} = 90^\circ ,\widehat {AED} = 90^\circ \)
Tứ giác \(EFGH\) có \(\widehat {AFB} = 90^\circ ,\widehat {DHC} = 90^\circ ,\widehat {AED} = 90^\circ \) nên \(EFGH\) là hình chữ nhật.
Xét \(\Delta ADE\) và \(\Delta BCG\) có:
\(\begin{array}{l}\widehat {ADE} = \widehat {GCB} = 45^\circ \\AD = BC\\\widehat {DAE} = \widehat {CBG} = 45^\circ \\ = > \Delta ADE = \Delta BCG\left( {g - c - g} \right)\\ = > AE = BG\end{array}\)
\(\Delta ABF\) cân ở \(F\) (vì \(\widehat {BAF} = \widehat {ABF} = 45^\circ \)) =>\(AF = BF\)
Ta có:
\(\left\{ \begin{array}{l}AF = AE + EF\\BF = BG + GF\end{array} \right.\) mà \(\left\{ \begin{array}{l}AE = BG\\AF = BF\end{array} \right.\), suy ra \(EF = GF\)
Hình chữ nhật \(EFGH\) có \(EF = GF\) nên \(EFGH\) là hình vuông