Giải bài 3. 9 trang 43 SGK Toán 10 tập 1 – Kết nối tri thức — Không quảng cáo

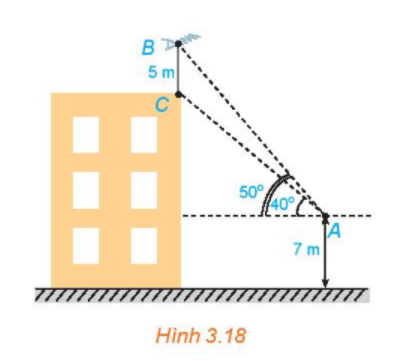
Trên nóc một tòa nhà có một cột ăng-ten cao 5m. Từ một vị trí quan sát A cao 7 m so với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng-ten, với các góc tương ứng là ${50^o}$và ${40^o}$ so với phương nằm ngang (H.3.18).

a)  Tính các góc của tam giác ABC.

b)  Tính chiều cao của tòa nhà.

LG a

a)  Tính các góc của tam giác ABC.

Phương pháp giải:

Nhắc lại: Tổng ba góc của một tam giác luôn bằng ${180^o}$.

Bước 1: Gọi H là hình chiếu của A lên đường thẳng BC.

Bước 2: Tính góc $\widehat {BAC}$, góc $\widehat {ABC}$ => góc $\widehat {BCA}$.

Lời giải chi tiết:

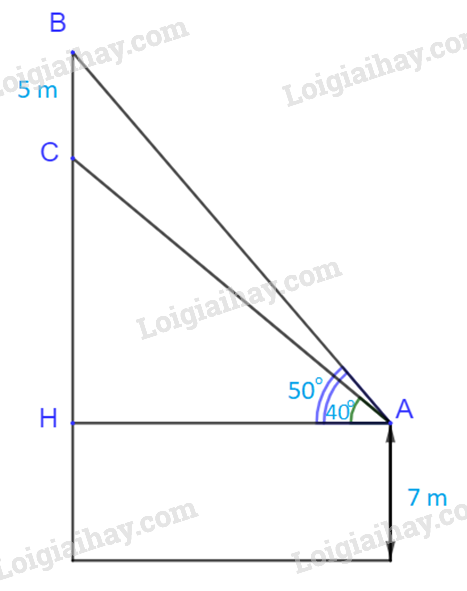
Gọi H là hình chiếu của A lên đường thẳng BC.

Ta có: $\widehat {HAB} = {50^o}$; $\widehat {HAC} = {40^o}$

$\Rightarrow \widehat {BAC} = {50^o} - {40^o} = {10^o}$ (1)

Xét tam giác ABH, vuông tại H ta có:

$\widehat H = {90^o};\;\widehat {BAH} = {50^o}.$

$\Rightarrow \widehat {HBA} = {180^o} - {90^o} - {50^o} = {40^o}$ hay $\widehat {CBA} = {40^o}$. (2)

Từ (1) và (2), suy ra: $\widehat {BCA} = {180^o} - {40^o} - {10^o} = {130^o}.$

Vậy ba góc của tam giác ABC lần lượt là: $\widehat A = {10^o};\;\widehat B = {40^o};\;\widehat C = {130^o}$.

LG b

b) Tính chiều cao của tòa nhà.

Phương pháp giải:

Bước 1: Tính AB: $AB = \frac{{BC.\sin C}}{{\sin A}}$

Bước 2:  Tính BH => chiều cao của tòa nhà = BH + độ cao của vị trí quan sát.

Lời giải chi tiết:

Áp dụng định lý sin cho tam giác ABC, ta được:

$\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}$ $\Rightarrow AB = \frac{{BC.\sin C}}{{\sin A}}$

Mà: $BC = 5\;(m);\;\;\widehat C = {130^o};\;\widehat A = {10^o}$

$\Rightarrow AB = \frac{{5.\sin {{130}^o}}}{{\sin {{10}^o}}} \approx 22\;(m)$

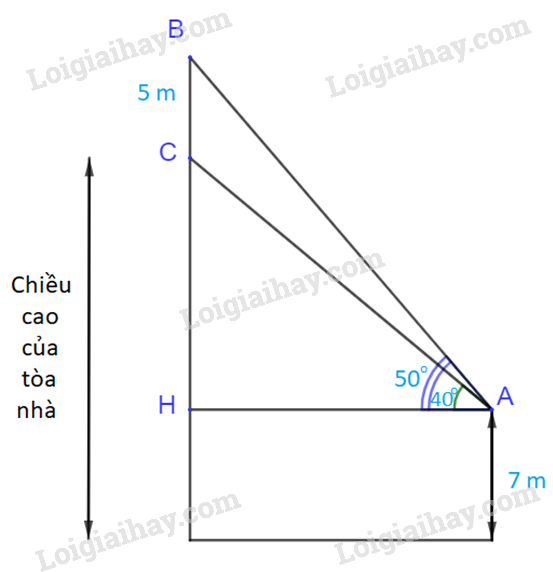
Xét tam giác ABH, vuông tại H ta có:

$\sin \widehat {BAH} = \frac{{BH}}{{AB}}$$\Rightarrow BH = AB.\,\,\sin \widehat {BAH}$

Mà: $AB \approx 22\;(m);\;\;\widehat {BAH} = {50^o}$

$\Rightarrow BH \approx 22.\sin {50^o} \approx 16,85\;(m)$

Vậy chiều cao của tòa nhà là: $BH-{\rm{ }}BC + 7 = 16,85-5 + 7 = 18,85{\rm{ }}\left( m \right)$