Giải bài 3 trang 116, 117 vở thực hành Toán 9 tập 2
Khi cho tam giác SOA vuông tại O quay quanh cạnh SO một vòng, ta được một hình nón. Biết (OA = 8cm), (SA = 17cm). a) Tính diện tích xung quanh của hình nón. b) Tính thể tích của hình nón.
Đề bài
Khi cho tam giác SOA vuông tại O quay quanh cạnh SO một vòng, ta được một hình nón. Biết \(OA = 8cm\), \(SA = 17cm\).
a) Tính diện tích xung quanh của hình nón.
b) Tính thể tích của hình nón.
Phương pháp giải - Xem chi tiết
a) Diện tích xung quanh của hình nón bán kính r và độ dài đường sinh l là: \({S_{xq}} = \pi rl\).
b) Thể tích của hình nón bán kính r và chiều cao h là: \(V = \frac{1}{3}\pi {r^2}h\).
Lời giải chi tiết
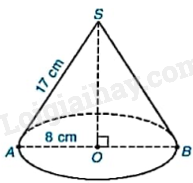
a) Diện tích xung quanh của hình nón là: \({S_{xq}} = \pi Rl = \pi .8.17 = 136\pi \left( {c{m^2}} \right)\).
b) Tam giác \(SOA\) vuông tại \(O\) nên theo định lí Pythagore ta có
\(S{O^2} + O{A^2} = S{A^2}\)
\(S{O^2} + {8^2} = {17^2}\)
\(S{O^2} = 289 - 64 = 225\)
\(SO = 15\)
Suy ra \(h = 15\)
Thể tích của hình nón là: \(V = \frac{1}{3}\pi .{R^2}.h = \frac{1}{3}\pi {.8^2}.15 = 320\pi \left( {c{m^3}} \right)\).