Giải Bài 3 trang 14 SGK Toán 8 tập 2 – Chân trời sáng tạo — Không quảng cáo

Đề bài

Vẽ một hệ trục tọa độ $Oxy$ và đánh dấu các điểm $A\left( { - 3;3} \right);B\left( {3;3} \right);C\left( {3; - 3} \right);D\left( { - 3; - 3} \right)$. Nêu nhận xét về các cạnh và góc của tứ giác ABCD.

Lời giải chi tiết

Điểm $A\left( { - 3;3} \right) \Rightarrow$ hoành độ là -3 và tung độ là 3.

Điểm $B\left( {3;3} \right) \Rightarrow$ hoành độ là 3 và tung độ là 3.

Điểm $C\left( {3; - 3} \right) \Rightarrow$ hoành độ là 3 và tung độ là -3.

Điểm $D\left( { - 3; - 3} \right) \Rightarrow$ hoành độ là -3 và tung độ là -3.

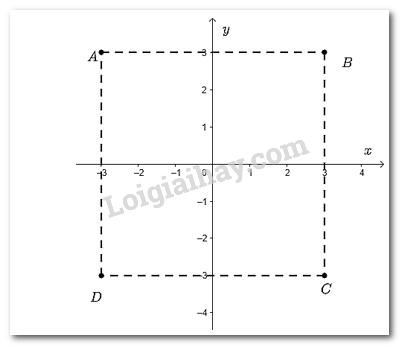
Các cạnh của tứ giác $ABCD$ bằng nhau và các góc của tứ giác $ABCD$ bằng nhau và bằng $90^\circ$.