Giải bài 3 trang 38 sách bài tập toán 9 - Chân trời sáng tạo tập 2 — Không quảng cáo

Đề bài

Trực ban ghi lại số ngày đi làm muộn của các công nhân một phân xưởng trong tháng 10 và tháng 11 ở bảng tần số sau.

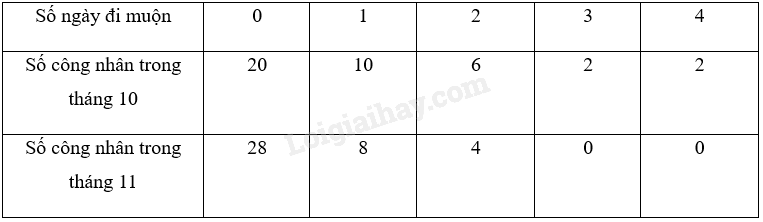
a) Hãy tính tần số tương đối của số ngày đi làm muộn của các công nhân trong tháng 10 và tháng 11.

b) Hãy lựa chọn và vẽ biểu đồ phù hợp để so sánh tình trạng đi làm muộn của các công nhân trong tháng 10 và tháng 11.

c) Có ý kiến cho rằng so với tháng 10, tình trạng đi muộn đã được cải thiện trong tháng 11. Ý kiến đó có hợp lí không? Tại sao?

Lời giải chi tiết

a) Số công nhân của phân xưởng trong tháng 10 là: 20 + 10 + 6 + 2 + 2 = 40 (công nhân).

Số công nhân của phân xưởng trong tháng 11 là: 28 + 8 + 4 = 40 (công nhân).

Vậy số công nhân của phân xưởng trong tháng 10 và tháng 11 đều là N = 40.

Gọi \({f_o},{f_1},{f_2},{f_3},{f_4}\) lần lượt là tần số tương đối của số ngày đi muộn là 0; 1; 2; 3; 4 của các công nhân trong tháng 10. Ta có:

\(\begin{array}{l}{f_o} = \frac{{20}}{{40}}.100\%  = 50\% ;{f_1} = \frac{{10}}{{40}}.100\%  = 25\% ;{f_2} = \frac{6}{{40}}.100\%  = 15\% ;\\{f_3} = \frac{2}{{40}}.100\%  = 5\% ;{f_4} = \frac{2}{{40}}.100\%  = 5\% .\end{array}\)

Gọi \({f_o}',{f_1}',{f_2}',{f_3}',{f_4}'\) lần lượt là tần số tương đối của số ngày đi muộn là 0; 1; 2; 3; 4 của các công nhân trong tháng 11. Ta có:

\(\begin{array}{l}{f_o}' = \frac{{28}}{{40}}.100\%  = 70\% ;{f_1}' = \frac{8}{{40}}.100\%  = 20\% ;\\{f_2}' = \frac{4}{{40}}.100\%  = 10\% ;{f_3}' = {f_4}' = 0\% .\end{array}\)

b) Để so sánh tình trạng đi làm muộn của các công nhân giữa tháng 10 và tháng 11, ta có thể sử dụng biểu đồ cột kép mô tả tần số tương đối của số ngày đi muộn.

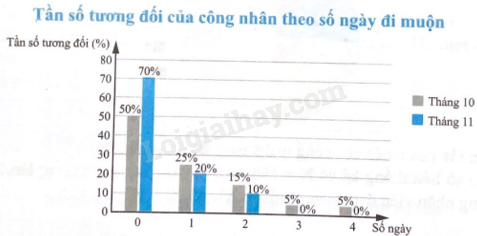
c) So với tháng 10, trong tháng 11, tần số tương đối của công nhân không đi làm muộn ngày nào tăng 20%; tần số tương đối của công nhân đi làm muộn 1 ngày và 2 ngày giảm; không còn công nhân đi muộn nhiều hơn 2 ngày. Vậy ý kiến  cho rằng so với tháng 10, tình trạng đi muộn đã được cải thiện trong tháng 11 là hợp lí.