Giải bài 3 trang 78 SGK Toán 7 tập 2 - Chân trời sáng tạo — Không quảng cáo

Đề bài

Cho tam giác ABC vuông cân tại A. Lấy điểm E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE. Chứng minh rằng:

a) DE vuông góc với BC                                b) BE vuông góc với DC

Lời giải chi tiết

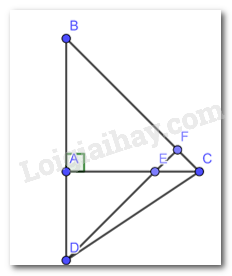
a) Vì tam giác ABC vuông cân tại A

$\Rightarrow$ $\widehat B = \widehat C = {45^o}$(2 góc ở đáy bằng nhau)

Xét tam giác AED có :

AE = AD

AC vuông góc với AB

$\Rightarrow$ Tam giác AED vuông cân tại A

$\Rightarrow \widehat {ADE} = \widehat {AED} = {45^o}$

Mà $\widehat {AED};\widehat {CEF}$là 2 góc đối đỉnh $\Rightarrow \widehat {AED} = \widehat {CEF} = {45^o}$

Xét tam giác CEF áp dụng định lí tổng 3 góc trong tam giác ta có :

$\Rightarrow \widehat F + \widehat C + \widehat E = {180^o}$

$\Rightarrow \widehat F = {180^o} - {45^o} - {45^o} = {90^o} \Rightarrow EF \bot BC \Rightarrow DE \bot BC$

b) Vì DE vuông góc với BC $\Rightarrow$ DE là đường cao của tam giác BCD

Vì AC cắt DE tại E nên E là trực tâm tam giác BCD (Do AC cũng là đường cao của tam giác BCD)

$\Rightarrow$BE cùng là đường cao của tam giác BCD (định lí 3 đường cao trong tam giác đi qua trực tâm)

$\Rightarrow$BE vuông góc với DC