Giải bài 3 trang 75 SGK Toán 7 tập 1 - Chân trời sáng tạo — Không quảng cáo

Đề bài

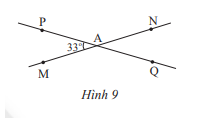
Cho đường thẳng MN, PQ cắt nhau tại A và tạọ thành $\widehat {PAM} = 33^\circ$ (Hình 9)

a) Tính số đo các góc còn lại.

b) Vẽ tia At là tia phân giác của $\widehat {PAN}$. Hãy tính số đo của $\widehat {tAQ}$. Vẽ At’ là tia đối của tia At. Giải thích tại sao At’ là tia phân giác của $\widehat {MAQ}$

Lời giải chi tiết

a) Ta có: $\widehat {PAM} = \widehat {QAN}$ ( 2 góc đối đỉnh) , mà $\widehat {PAM} = 33^\circ$nên $\widehat {QAN} = 33^\circ$

Vì $\widehat {PAN} + \widehat {PAM} = 180^\circ$ ( 2 góc kề bù) nên $\widehat {PAN} + 33^\circ  = 180^\circ  \Rightarrow \widehat {PAN} = 180^\circ  - 33^\circ  = 147^\circ$

Vì $\widehat {PAN} = \widehat {QAM}$( 2 góc đối đỉnh) , mà $\widehat {PAN} = 147^\circ$ nên $\widehat {QAM} = 147^\circ$

b)

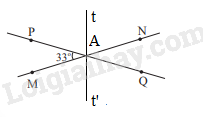
Vì At là tia phân giác của $\widehat {PAN}$ nên $\widehat {PAt} = \widehat {tAN} = \frac{1}{2}.\widehat {PAN} = \frac{1}{2}.147^\circ  = 73,5^\circ$

Vì $\widehat {tAQ} + \widehat {PAt} = 180^\circ$ ( 2 góc kề bù) nên $\widehat {tAQ} + 73,5^\circ  = 180^\circ  \Rightarrow \widehat {tAQ} = 180^\circ  - 73,5^\circ  = 106,5^\circ$

Vẽ At’ là tia đối của tia At, ta được $\widehat {QAt'} = \widehat {PAt}$( 2 góc đối đỉnh)

Ta có: $\widehat {QAt'} = \widehat {MAt'} = \frac{1}{2}.\widehat {MAQ}$ nên At’ là tia phân giác của $\widehat {MAQ}$

Chú ý:

2 tia phân giác của 2 góc đối đỉnh là 2 tia đối nhau