Giải bài 3 trang 8 sách bài tập toán 11 - Chân trời sáng tạo tập 1
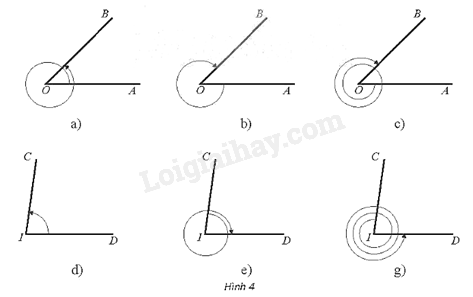
Xác định số đo của các góc lượng giác được biểu diễn trong mỗi hình dưới đây. Biết trong các Hình 4a, b, c có \(\widehat {AOB} = \frac{\pi }{4}\); trong Hình 4d, e, g có \(\widehat {CID} = {82^0}\).
Đề bài
Xác định số đo của các góc lượng giác được biểu diễn trong mỗi hình dưới đây. Biết trong các Hình 4a, b, c có \(\widehat {AOB} = \frac{\pi }{4}\); trong Hình 4d, e, g có \(\widehat {CID} = {82^0}\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về khái niệm góc lượng giác:
a, b, c) Số đo của các góc lượng giác có cùng tia đầu Oa và tia cuối Ob sai khác nhau một bội nguyên của \({360^0}\) nên có công thức tổng quát là: \(\left( {Oa,Ob} \right) = {\alpha ^0} + k{360^0}\left( {k \in \mathbb{Z}} \right)\) với \({\alpha ^0}\) là số đo của một góc lượng giác bất kì có tia đầu Oa và tia cuối Ob.
d, e, g) Số đo của các góc lượng giác có cùng tia đầu Oa và tia cuối Ob sai nhau khác một bội nguyên của \(2\pi \) nên ta có công thức tổng quát là \(\left( {Oa,Ob} \right) = \alpha + k2\pi \left( {k \in \mathbb{Z}} \right)\) với \(\alpha \) là số đo theo radian của một góc lượng giác bất kì có tia đầu Oa và tia cuối Ob.
Lời giải chi tiết

Số đo của góc lượng giác (OA, OB) trong Hình 4a là: \(\frac{\pi }{4} + 2\pi = \frac{{9\pi }}{4}\)
Số đo của góc lượng giác (OA, OB) trong Hình 4b là: \(\frac{\pi }{4} - 2\pi = - \frac{{7\pi }}{4}\)
Số đo của góc lượng giác (OA, OB) trong Hình 4c là: \(\frac{\pi }{4} - 2.2\pi = \frac{{ - 15\pi }}{4}\)
Số đo của góc lượng giác (IC, ID) trong Hình 4d là: \({82^0}\)
Số đo của góc lượng giác (IC, ID) trong Hình 4e là: \( - \left( {{{82}^0} + {{360}^0}} \right) = - {442^0}\)
Số đo của góc lượng giác (IC, ID) trong Hình 4g là: \({360^0} - {82^0} + {2.360^0} = {998^0}\)