Giải Bài 36 trang 78 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC có góc A nhỏ hơn 90°. Lấy hai điểm M, N nằm ngoài tam giác ABC sao cho MA vuông góc với AB, NA vuông góc với AC và MA = AB, NA = AC. Gọi I, K lần lượt là giao điểm của BN với AC, MC (Hình 24).
Đề bài
Cho tam giác ABC có góc A nhỏ hơn 90°. Lấy hai điểm M, N nằm ngoài tam giác ABC sao cho MA vuông góc với AB, NA vuông góc với AC và MA = AB, NA = AC. Gọi I, K lần lượt là giao điểm của BN với AC, MC ( Hình 24 ).
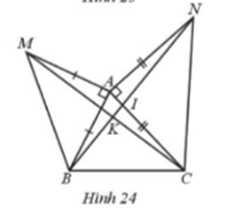
Chứng minh:
a) ∆AMC = ∆ABN;
b) BN vuông góc với CM.
Phương pháp giải - Xem chi tiết
- Xét các điều kiện về cạnh và góc để chứng minh ∆AMC = ∆ABN
- Từ hai tam giác bằng nhau suy ra các góc tương ứng bằng nhau để chứng minh cho BN vuông góc với CM.
Lời giải chi tiết
a) Ta có:
\(\widehat {MAC} = \widehat {MAB} + \widehat {BAC} = 90^\circ + \widehat {BAC}\)
\(\widehat {MAC} = \widehat {MAB} + \widehat {BAC} = 90^\circ + \widehat {BAC}\)
Suy ra: \(\widehat {MAC} = \widehat {NAB}\)
Xét ∆AMC và ∆ABN có:
MA = AB (giả thiết),
\(\widehat {MAC} = \widehat {NAB}\) (chứng minh trên),
AC = AN (giả thiết)
Suy ra ∆AMC = ∆ABN (c.g.c).
Vậy ∆AMC = ∆ABN.
b) Do ∆AMC = ∆ABN (chứng minh câu a)
Suy ra \(\widehat {ACM} = \widehat {ANB}\) (hai góc tương ứng).
Mặt khác, \(\widehat {KIC} + \widehat {AIN}\) (đối đỉnh).
Suy ra \(\widehat {ACM} + \widehat {KIC} = \widehat {ANB} + \widehat {AIN}\)
Xét ∆AIN vuông tại A có: \(\widehat {ANI} + \widehat {AIN} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Hay \(\widehat {ANB} + \widehat {AIN} = {90^o}\)
Do đó \(\widehat {ACM} + \widehat {KIC} = 90^\circ \) hay \(\widehat {ICK} + \widehat {KIC} = 90^\circ \)
Xét ∆KIC, có: \(\widehat {ICK} + \widehat {KIC} + \widehat {IKC} = 180^\circ \) (tổng ba góc của một tam giác).
Suy ra \(\widehat {IKC} = 180^\circ - \left( {\widehat {ICK} + \widehat {KIC}} \right) = 180^\circ - 90^\circ = 90^\circ \)
Do đó BN vuông góc với MC.
Vậy BN vuông góc với MC.