Giải bài 42 trang 60 SBT toán 10 - Cánh diều — Không quảng cáo

Đề bài

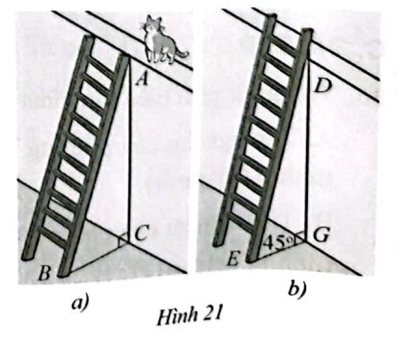
Để lao lên một bức tường, bác Dũng dùng một chiếc thang cao hơn bức tường đó 2m. Ban đầu bác Dũng đạt chiếc thang mà đầu trên của chiếc thang đó vừa chạm đúng vào mép trên của bức tường (Hình 21a). Sau đó bác Dũng dịch chuyển chân thang vào gần chân bức tường thêm 1 m thì bác Dũng thấy thang tạo với mặt đất một góc \({45^ \circ }\). Bức tường cao bao nhiêu mét?

Lời giải chi tiết

Gọi chiều cao bức tường là \(x\) (m) (\(x > 0\)).

Suy ra chiều dài của thang là \(x + 2\) (m)

Ta có: \(AC = x,AB = x + 2\)

Khi đặt chiếc thang mà đầu trên của chiếc thang đó chạm đúng vào mép trên của bức tường thì khoảng cách chân thang đến chân tường là: \(BC = \sqrt {A{B^2} - A{C^2}}  = \sqrt {{{\left( {x + 2} \right)}^2} - {x^2}} \) (m)

Khi dịch chuyển chân thang vào gần chân bức tường thêm 1m thì

\(EG = \sqrt {{{\left( {x + 2} \right)}^2} - {x^2}}  - 1\)

Khi ấy thang tạo với mặt đất góc \({45^ \circ }\) nên khoảng cách từ chân thang đến chân tường bằng chiều cao bức tường hay \(EG = x\)

Ta có phương trình \(\sqrt {{{\left( {x + 2} \right)}^2} - {x^2}}  - 1 = x \Leftrightarrow \sqrt {{{\left( {x + 2} \right)}^2} - {x^2}}  = x + 1\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x + 1 \ge 0\\{\left( {x + 2} \right)^2} - {x^2} = {\left( {x + 1} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge  - 1\\4x + 4 = {x^2} + 2x + 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge  - 1\\{x^2} - 2x - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge  - 1\\\left[ \begin{array}{l}x =  - 1\;(L)\\x = 3\;\end{array} \right.\quad \end{array} \right. \Leftrightarrow x = 3\;\end{array}\)

Vậy, chiều cao của bức tường là 3 m.