Giải bài 5 trang 58 SGK Toán 7 tập 2 - Chân trời sáng tạo
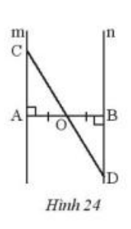
Cho đoạn thẳng AB có O là trung điểm. Vẽ hai đường thẳng m và n lần lượt vuông góc với AB tại A và B. Lấy điểm C trên m, CO cắt n tại D (Hình 24). Chứng minh rằng O là trung điểm CD.
Đề bài
Cho đoạn thẳng AB có O là trung điểm. Vẽ hai đường thẳng m và n lần lượt vuông góc với AB tại A và B. Lấy điểm C trên m, CO cắt n tại D (Hình 24). Chứng minh rằng O là trung điểm CD.
Phương pháp giải - Xem chi tiết
- Chứng minh tam giác OAC và tam giác OBD bằng nhau
- Từ đó suy ra OC = OD ( 2 cạnh tương ứng)
Lời giải chi tiết
Xét \(\Delta OAC\) và \(\Delta OBD\), ta có:
\(\widehat {COA} = \widehat {BOD}\) ( 2 góc đối đỉnh)
AO = BO
\(\widehat A = \widehat B\)
\(\Rightarrow \Delta OAC=\Delta OBD\) ( g-c-g )
\( \Rightarrow CO = DO\) ( cạnh tương ứng )
\( \Rightarrow \) O là trung điểm CD
Cùng chủ đề:
Giải bài 5 trang 58 SGK Toán 7 tập 2 - Chân trời sáng tạo