Giải bài 5 trang 64 vở thực hành Toán 8 — Không quảng cáo

Đề bài

Cho hình vuông ABCD. Trên cạnh BC lấy điểm N. Từ A kẻ đường thẳng vuông góc với AN cắt đường thẳng CD tại Q. Gọi I là trung điểm của NQ. Gọi M là giao điểm AI và CD. Qua N dựng đường thẳng song song với CD cắt AI tại P. Chứng minh rằng:

a) ∆PIN = ∆MIQ.

b) Tứ giác MNPQ là hình thoi.

Lời giải chi tiết

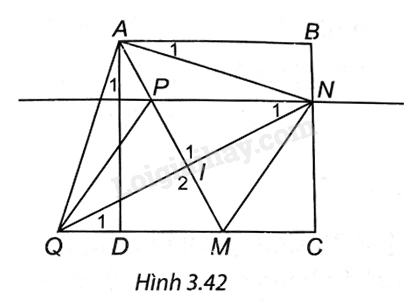
(H.3.42). a) Xét hai tam giác PIN và MIQ có ${\widehat I_1} = {\widehat I_2}$ (hai góc đối đỉnh), QI = IN, ${\widehat N_1} = {\widehat Q_1}$ (do NP // QM)

⇒ ∆PIN = ∆MIQ (g.c.g)

⇒ QM = NP.

b) Tứ giác MNPQ có PN // MQ, QM = NP nên là hình bình hành.

Ta chứng minh MNPQ có hai đường chéo vuông góc.

Vì AQ ⊥ AN nên ${\widehat A_1} + \widehat {DAN} = 90^\circ ,\,\,{\widehat A_2} + \widehat {DAN} = 90^\circ$ Xét hai tam giác vuông ADQ và ABN có AD = AB, ${\widehat A_1} = {\widehat A_2}.$ (chứng minh trên).

⇒ ∆ADQ = ∆ABN (cạnh góc vuông – góc nhọn)

⇒ AQ = AN.

Do đó tam giác AQN cân tại A, mà AI là đường trung tuyến của tam giác AQN

⇒ AI là đường cao của tam giác AQN, tức là AI ⊥ QN, hay PM ⊥ QN.

Hình bình hành MNPQ có hai đường chéo PM ⊥ QN nên là hình thoi.