Giải bài 5 trang 69 SGK Toán 8 – Cánh diều — Không quảng cáo

Đề bài

Cho tam giác ABC vuông tại A có AB = 3, AC = 4, AD là đường phân giác. Tính:

a) Độ dài các đoạn thẳng BC, DB, DC;

b) Khoảng cách từ điểm D đến đường thẳng AC;

c) Độ dài đường phân giác AD

Lời giải chi tiết

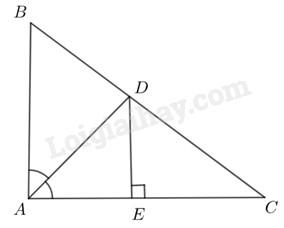
a)      Tam giác ABC vuông tại A nên ta có:

\(BC = \sqrt {A{B^2} + A{C^2}}  = \sqrt {{3^2} + {4^2}}  = 5\)

Vì AD là đường phân giác của tam giác ABC nên ta có:

\(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\) (Tính chất đường phân giác trong tam giác)

\( \Rightarrow \frac{{DB}}{{DC}} = \frac{3}{4} \Rightarrow DB = \frac{3}{4}DC\)

Mà \(BD + CD = BC \Rightarrow \frac{3}{4}CD + CD = 5 \Rightarrow CD = \frac{{20}}{7}\)

\( \Rightarrow BD = 5 - \frac{{20}}{7} = \frac{{15}}{7}\).

b)     Từ D kẻ đường thẳng vuông góc với AC cắt AC tại E. Khi đó DE là khoảng cách từ D đến đường thẳng AC.

Ta có: \(\left. \begin{array}{l}DE \bot AC\\AB \bot AC\end{array} \right\} \Rightarrow DE// AB\)

\( \Rightarrow \frac{{DE}}{{AB}} = \frac{{DC}}{{BC}} \Rightarrow \frac{{DE}}{3} = \frac{{\frac{{20}}{7}}}{5} \Rightarrow DE = \frac{{12}}{7}\) (Tính chất đường phân giác)

c)      Xét tam giác ABC có \(DE// AB\) nên \(\frac{{BD}}{{BC}} = \frac{{AE}}{{AC}}\) (Định lý Thales)

\( \Rightarrow \frac{{\frac{{15}}{7}}}{5} = \frac{{AE}}{4} \Rightarrow AE = \frac{{12}}{7}\)

Tam giác ADE vuông tại E nên ta có:

\(AD = \sqrt {A{E^2} + D{E^2}}  = \sqrt {{{\left( {\frac{{12}}{7}} \right)}^2} + {{\left( {\frac{{12}}{7}} \right)}^2}}  = \frac{{12\sqrt 2 }}{7}\)