Giải bài 5 trang 78 SGK Toán 8 – Cánh diều
Bạn Hoa vẽ trên giấy một tam giác ABC và đoạn thẳng MN
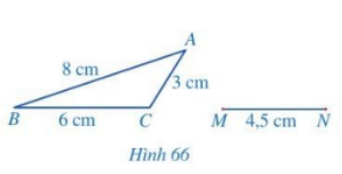
Đề bài
Bạn Hoa vẽ trên giấy một tam giác ABC và đoạn thẳng MN với các kích thước như Hình 66 . Bạn Hoa đố bạn Thanh vẽ điểm P thỏa mãn \(\widehat {PMN} = \widehat {ACB},\,\,\widehat {PNM} = \widehat {BAC}\) mà không sử dụng thước đo góc. Em hãy giúp bạn Thanh sử dụng thước thẳng (có chia khoảng milimét) và compa để vẽ điểm P và giải thích kết quả tìm được.
Phương pháp giải - Xem chi tiết
Sử dụng định nghĩa tam giác đồng dạng để tìm điểm P.
Lời giải chi tiết
Vì tổng ba góc trong một tam giác bằng \(180^\circ \) nên nếu \(\widehat {PMN} = \widehat {ACB},\,\,\widehat {PNM} = \widehat {BAC}\) thì \(\widehat {MPN} = \widehat {CBA}\)
Ta cần \(\Delta ABC \backsim\Delta NPM\)
Khi đó \(\frac{{AB}}{{NP}} = \frac{{BC}}{{PM}} = \frac{{AC}}{{NM}}\) hay \(\frac{8}{{NP}} = \frac{6}{{PM}} = \frac{3}{{4,5}} = \frac{2}{3}\)
Ta có: \(\frac{8}{{NP}} = \frac{2}{3} \Rightarrow NP = 8.3:2 = 12cm\)
\(\frac{6}{{MP}} = \frac{2}{3} \Rightarrow MP = 6.3:2 = 9cm\)
Qua điểm N vẽ cung tròn tâm N, bán kính 12cm.
Qua điểm M vẽ cung tròn tâm M, bán kính 9cm.
Giao điểm của hai cung tròn vừa vẽ là điểm P. Ta có NP = 12cm và MP = 9cm.
Vậy Thanh chỉ cần thước thẳng và compa để xác định được điểm P thỏa mãn đề bài.