Giải bài 5 trang 72 sách bài tập toán 8 - Chân trời sáng tạo — Không quảng cáo

Đề bài

Cho hình vuông ABCD. Lấy E, F, G, H theo thứ tự thuộc các cạnh AB, BC, CD, DA sao cho \(AE = BF = CG = DH = a\); \(BE = CF = DG = AH = b\). Chứng minh rằng:

a) Tứ giác EFGH là hình gì?

b) Tính diện tích tứ giác EFGH theo a và b.

Lời giải chi tiết

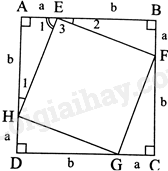
Vì ABCD là hình vuông nên \(\widehat A = \widehat B = \widehat C = \widehat D = {90^0}\)

Tam giác HAE và tam giác EBF có:

\(\widehat A = \widehat B = {90^0},AE = BF\left( { = a} \right),AH = BE\left( { = b} \right)\)

Do đó, \(\Delta HAE = \Delta EBF\left( {cgv - cgv} \right)\), suy ra \(HE = FE\), \(\widehat {{H_1}} = \widehat {{E_2}}\)

Chứng minh tương tự ta có:

\(\Delta HAE = \Delta GDH\left( {cgv - cgv} \right)\) nên \(HE = HG\)

\(\Delta FCG = \Delta GDH\left( {cgv - cgv} \right)\) nên \(GF = HG\)

Do đó, \(HE = FE = HG = GF\). Suy ra, tứ giác EFGH là hình thoi (1)

Ta có: \(\widehat {{E_2}} + \widehat {{E_1}} = \widehat {{H_1}} + \widehat {{E_1}} = {90^0}\). Do đó, \(\widehat {{E_3}} = {90^0}\) (2)

Từ (1) và (2) suy ra: Tứ giác EFGH là hình vuông.

b) Diện tích hình vuông ABCD là: \({S_{ABCD}} = A{B^2} = {\left( {a + b} \right)^2}\)

Diện tích tam giác vuông AHE là: \({S_{AHE}} = \frac{1}{2}AH.AE = \frac{1}{2}ab\)

Tương tự ta có: \({S_{HGD}} = {S_{GFC}} = {S_{EBF}} = \frac{1}{2}ab\)

Do đó: \({S_{EFGH}} = {S_{ABCD}} - \left( {{S_{HGD}} + {S_{GFC}} + {S_{EBF}} + {S_{AHE}}} \right)\)

\( = {\left( {a + b} \right)^2} - 4.\frac{1}{2}ab = {a^2} + 2ab + {b^2} - 2ab = {a^2} + {b^2}\)