Giải bài 5 trang 60 sách bài tập toán 8 - Chân trời sáng tạo — Không quảng cáo

Đề bài

Cho tam giác ABC cân tại A. Trên tia đối của tia AB lấy điểm M, trên tia đối của tia AC lấy điểm N sao cho $AM = AN.$ Chứng minh tứ giác MNBC là hình thang cân.

Lời giải chi tiết

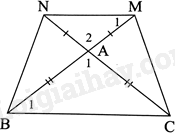
Vì tam giác ABC cân tại A nên $AB = AC$ và $\widehat {{B_1}} = \widehat {ACB}$, mà $\widehat {{B_1}} + \widehat {ACB} + \widehat {{A_1}} = {180^0}$. Do đó, $\widehat {{B_1}} = \frac{{{{180}^0} - \widehat {{A_1}}}}{2}$ (1)

Vì $AM = AN\left( {gt} \right)$ nên tam giác AMN cân tại A.

Do đó, $\widehat {{M_1}} = \widehat {ANM}$, mà $\widehat {{M_1}} + \widehat {ANM} + \widehat {{A_2}} = {180^0}$

Do đó, $\widehat {{M_1}} = \frac{{{{180}^0} - \widehat {{A_2}}}}{2}$ (2)

Lại có: $\widehat {{A_1}} = \widehat {{A_2}}$ (hai góc đối đỉnh) (3)

Từ (1), (2), (3) ta có: $\widehat {{B_1}} = \widehat {{M_1}}$, mà hai góc này ở vị trí so le trong nên MN//BC. Do đó, tứ giác MNBC là hình thang (5).

Ta có: $AM = AN\left( {gt} \right)$, $AB = AC$(cmt) nên $AM + AB = AN + AC$, suy ra $BM = CN$ (6)

Từ (5) và (6) ta có: Tứ giác MNBC là hình thang cân.