Giải bài 5 trang 77 vở thực hành Toán 7
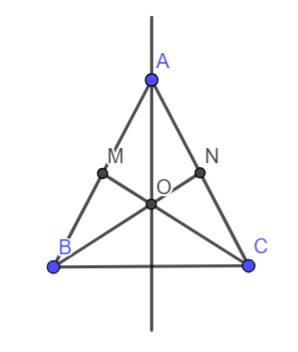
Bài 5. Cho tam giác ABC cân tại A. Gọi M, N lần lượt là trung điểm AB, AC. Gọi O là giao diểm của đường thẳng BN và CM. Chứng minh rằng O nằm trên đường trung trực của đoạn thẳng BC.
Đề bài
Bài 5. Cho tam giác ABC cân tại A. Gọi M, N lần lượt là trung điểm AB, AC. Gọi O là giao diểm của đường thẳng BN và CM. Chứng minh rằng O nằm trên đường trung trực của đoạn thẳng BC.
Phương pháp giải - Xem chi tiết
Chứng minh OB = OC
Lời giải chi tiết
|
GT |
\(\Delta ABC\)cân tại A,\(M \in AC,N \in AC,AM = MB,\) \(AN = NC,BN \cap CM = O.\) |
|
KL |
O thuộc trung trực BC |
Hai tam giác ABN và ACM có:
AB = AC (\(\Delta ABC\)cân tại A)
\(\widehat {BAN} = \widehat {CAM}\)(góc chung)
\(AN = \frac{{AC}}{2} = \frac{{AB}}{2} = AM\)(\(\Delta ABC\)cân tại A)
Vậy \(\Delta ABN = \Delta ACM\)(c-g-c). Từ đó suy ra \(\widehat {ABN} = \widehat {ACM},\widehat {ANB} = \widehat {AMC}\)
Hai tam giác BOM và CON có:
\(\widehat {OMB} = {180^o} - \widehat {AMC} = {180^o} - \widehat {ANB} = \widehat {ONC}\)(chứng minh trên)
\(BM = \frac{{AB}}{2} = \frac{{AC}}{2} = CN\)(\(\Delta ABC\)cân tại A)
\(\widehat {MBO} = \widehat {ABN} = \widehat {ACM} = \widehat {NCO}\)(chứng minh trên)
Vậy \(\Delta BOM = \Delta CON\)(g-c-g). Do đó OB = OC.
Vậy O cách đều hai đầu của đoạn thẳng BC. Suy ra O nằm trên trung trực của BC.