Giải bài 5 trang 68 vở thực hành Toán 7
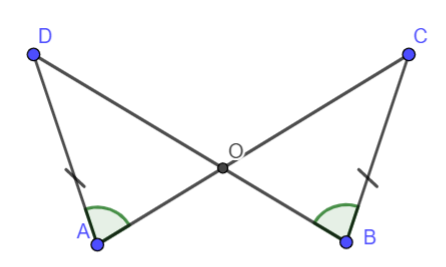
Bài 5. Cho hình vẽ dưới đây. Biết rằng AD = BC, \(\widehat {DAC} = \widehat {CBD}\), O là giao điểm của AC và BD. Chứng minh rằng AO = BO.
Đề bài
Bài 5. Cho hình vẽ dưới đây. Biết rằng AD = BC, \(\widehat {DAC} = \widehat {CBD}\), O là giao điểm của AC và BD. Chứng minh rằng AO = BO.
Phương pháp giải - Xem chi tiết
Chứng minh hai tam giác AOD và BOC bằng nhau
Lời giải chi tiết
Ta có \(\widehat {AOD} = \widehat {BOC}\)(hai góc đối đỉnh).
Do tổng các góc trong mỗi tam giác ADO và BCO bằng \({180^o}\) nên ta có
\(\widehat {ADO} = {180^o} - \widehat {DOA} - \widehat {DAO} = {180^o} - \widehat {BOC} - \widehat {CBO} = \widehat {BCO}\)
Hai tam giác AOD và BOC có
\(\widehat {ADO} = \widehat {BCO}\)(chứng minh trên)
AD = BC (theo giả thiết)
\(\widehat {DAO} = \widehat {DAC} = \widehat {CBD} = \widehat {CBO}\)(theo giả thiết)
Vậy \(\Delta AOD = \Delta BOC\)(g – c – g ). Do đó AO = BO.