Giải bài 57 trang 124 sách bài tập toán 9 - Cánh diều tập 1
Cho hình thang vuông ABCD (\(\widehat A = \widehat B = 90^\circ \)) với \(\widehat C = 30^\circ \), BC = CD = a. Vẽ một phần đường tròn (C; CD) (Hình 54). Tính diện tích của phần tô màu xám theo a.
Đề bài
Cho hình thang vuông ABCD (\(\widehat A = \widehat B = 90^\circ \)) với \(\widehat C = 30^\circ \), BC = CD = a. Vẽ một phần đường tròn (C; CD) (Hình 54). Tính diện tích của phần tô màu xám theo a.
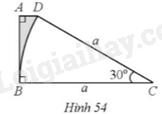
Phương pháp giải - Xem chi tiết
Diện tích của phần tô màu xám = diện tích hình thang ABCD – diện tích quạt tròn CBD.
Bước 1: Áp dụng tỉ số lượng giác để tính DH, CH; từ đó tính được BH.
Bước 2: Chứng minh ABHD là hình chữ nhật, từ đó tính được AB, AD.
Bước 3: Tính diện tích hình thang ABCD, diện tích quạt tròn CBD.
Lời giải chi tiết
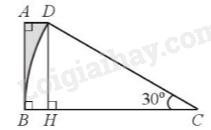
Kẻ \(DH \bot BC\)(\(H \in BC\)) suy ra \(\widehat {CHD} = \widehat {BHD} = 90^\circ \).
Do tam giác CDH vuông tại H nên ta có \(DH = CD.\sin C = a.\sin 30^\circ = a.\frac{1}{2} = \frac{a}{2}\)
và \(CH = CD.\cos C = a.\cos 30^\circ = \frac{{a\sqrt 3 }}{2}\)
Ta có \(BH = BC - CH = a - \frac{{a\sqrt 3 }}{2} = \frac{{a\left( {2 - \sqrt 3 } \right)}}{2}\)
Xét tứ giác ABHD có: \(\widehat A = \widehat B = \widehat {BHD} = 90^\circ \) nên ABHD là hình chữ nhật,
do đó \(AB = DH = \frac{a}{2}\), \(AD = BH = \frac{{a\left( {2 - \sqrt 3 } \right)}}{2}\)
Diện tích hình thang ABCD là
\({S_1} = \frac{{AB\left( {AD + BC} \right)}}{2} = \frac{a}{2}.\left( {\frac{{a\left( {2 - \sqrt 3 } \right)}}{2} + a} \right):2 = \frac{{{a^2}\left( {4 - \sqrt 3 } \right)}}{8}\)
Diện tích quạt tròn BCD là
\({S_2} = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi .{a^2}.30}}{{360}} = \frac{{\pi {a^2}}}{{12}}\)
Diện tích phần tô xám là
\(S = {S_1} - {S_2} = \frac{{{a^2}\left( {4 - \sqrt 3 } \right)}}{8} - \frac{{\pi {a^2}}}{{12}} = \frac{{{a^2}\left( {12 - 3\sqrt 3 - 2\pi } \right)}}{{24}}\).