Giải Bài 58 trang 86 sách bài tập toán 7 - Cánh diều — Không quảng cáo

Đề bài

Cho tam giác ABC vuông tại A (AB < AC), BD là tia phân giác của góc ABC (D ∈ AC). Qua C kẻ tia Cx vuông góc với AC cắt BD tại M.

a) Chứng minh tam giác CBM là tam giác cân.

b) So sánh độ dài CM và AC.

Lời giải chi tiết

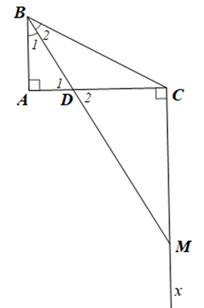
a) Vì ∆ABD vuông tại A nên ${\hat B_1} + {\hat D_1} = 90^\circ$ (trong tam giác vuông, tổng hai góc nhọn bằng 90 ^o )

Mà ${\hat B_1} = {\hat B_2}$ (do BD là tia phân giác của góc ABC) và ${\hat D_1} = {\hat D_2}$ (hai góc đối đỉnh).

Nên ${\hat B_2} + {\hat D_2} = 90^\circ$

Vì ∆CDM vuông tại C nên $\hat M + {\hat D_2} = 90^\circ$ (trong tam giác vuông, tổng hai góc nhọn bằng 90 ^o ).

Suy ra $\hat M = {\hat B_2}$

Do đó tam giác CBM cân tại C.

Vậy tam giác CBM cân tại C.

b) Vì tam giác CBM cân tại C (chứng minh câu a)

Nên CM = BC.

Vì ∆ABC vuông tại A nên BC > AC (trong tam giác vuông, cạnh huyển là cạnh lớn nhất).

Suy ra CM > AC.

Vậy CM > AC.