Giải bài 6 trang 57 sách bài tập toán 8 - Chân trời sáng tạo
Cho tứ giác ABCD có (AB = AD,CB = CD,widehat C = {65^0},widehat A = {115^0})
Đề bài
Cho tứ giác ABCD có \(AB = AD,CB = CD,\widehat C = {65^0},\widehat A = {115^0}\)
a) Chứng minh AC là đường trung trực của BD.
b) Tính số đo góc B và góc D.
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về đường trung trực để chứng minh: Điểm cách đều hai đầu mút đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
b) Sử dụng kiến thức về tổng các góc của một tứ giác để tính góc: Tổng số đo các góc của một tứ giác bằng 360 độ.
Lời giải chi tiết
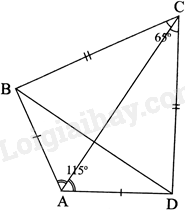
a) Vì \(AB = AD\) nên điểm A nằm trên đường trung trực của đoạn thẳng BD.
Vì \(CB = CD\) nên điểm C nằm trên đường trung trực của đoạn thẳng BD.
Do đó, AC là đường trung trực của BD
b) Tam giác ABC và tam giác ADC có:
\(AB = AD\), \(CB = CD\), AC chung
Do đó, \(\Delta ABC = \Delta ADC\left( {c.c.c} \right)\). Do đó, \(\widehat {ABC} = \widehat {ADC}\)
Tứ giác ABCD có: \(\widehat {ABC} + \widehat {ADC} + \widehat {BAD} + \widehat {BCD} = {360^0}\)
\(\widehat {ABC} + \widehat {ABC} = {360^0} - \widehat {DAB} - \widehat {BCD} = {180^0}\)
Do đó, \(\widehat {ABC} = {180^0}:2 = {90^0}\) nên \(\widehat {ADC} = {90^0}\)