Giải bài 6 trang 60 sách bài tập toán 8 - Chân trời sáng tạo tập 2
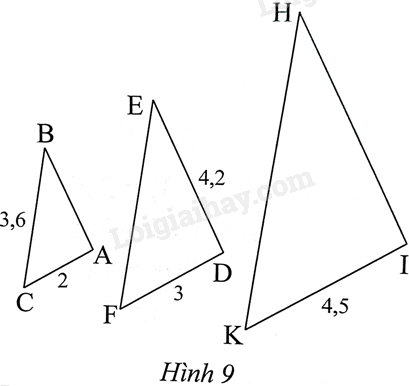
Trong Hình 9, cho biết $\Delta ABC\backsim \Delta DEF$, $\Delta DEF\backsim \Delta IHK$. Tính độ dài các đoạn thẳng AB, EF, IH và HK.
Đề bài
Trong Hình 9, cho biết $\Delta ABC\backsim \Delta DEF$, $\Delta DEF\backsim \Delta IHK$. Tính độ dài các đoạn thẳng AB, EF, IH và HK.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về định nghĩa hai tam giác đồng dạng để tính: Tam giác A’B’C’ gọi là đồng dạng với tam giác ABC nếu \(\widehat {A'} = \widehat A,\widehat {B'} = \widehat B,\widehat {C'} = \widehat C,\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\) (k gọi là tỉ số đồng dạng)
Lời giải chi tiết
Vì $\Delta ABC\backsim \Delta DEF$ nên \(\frac{{AB}}{{DE}} = \frac{{BC}}{{EF}} = \frac{{AC}}{{DF}}\), hay \(\frac{{AB}}{{4,2}} = \frac{{3,6}}{{EF}} = \frac{2}{3}\), suy ra \(AB = 2,8;EF = 5,4\)
Vì $\Delta DEF\backsim \Delta IHK$ nên \(\frac{{DE}}{{IH}} = \frac{{EF}}{{HK}} = \frac{{DF}}{{IK}}\), hay \(\frac{{4,2}}{{IH}} = \frac{{5,4}}{{HK}} = \frac{3}{{4,5}}\), suy ra \(IH = 6,3;HK = 8,1\)