Giải bài 6 trang 69 SGK Toán 8 – Cánh diều
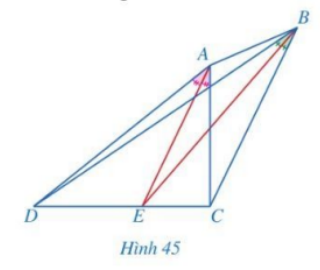
Cho tứ giác ABCD với các tia phân giác của các góc CAD và CBD cùng đi qua điểm E thuộc cạnh CD (Hình 45).
Đề bài
Cho tứ giác ABCD với các tia phân giác của các góc CAD và CBD cùng đi qua điểm E thuộc cạnh CD ( Hình 45 ). Chứng minh \(AD.BC{\rm{ }} = {\rm{ }}AC.BD\).
Phương pháp giải - Xem chi tiết
Sử dụng định lý đường trung bình để chứng minh theo yêu cầu đề bài.
Lời giải chi tiết
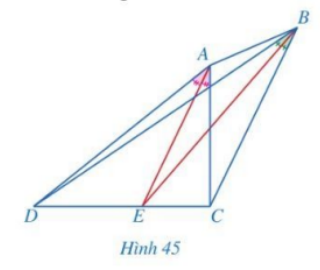
Xét tam giác ACD với đường phân giác AE, ta có:
\(\frac{{ED}}{{EC}} = \frac{{AD}}{{AC}}\,\,\left( 1 \right)\) (Tính chất đường phân giác trong tam giác)
Xét tam giác BCD với đường phân giác BE, ta có:
\(\frac{{ED}}{{EC}} = \frac{{BD}}{{BC}}\,\,\left( 2 \right)\) (Tính chất đường phân giác trong tam giác)
Từ (1) và (2) ta có: \(\frac{{AD}}{{AC}} = \frac{{BD}}{{BC}} \Rightarrow AD.BC = AC.BD\)