Giải bài 6 trang 85 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cho hai điểm A, B trên đường tròn (O; R). Cho biết AB = 9 cm và khoảng cách từ O đến đường thẳng AB là OH = (frac{R}{2}). Tính: a) Số đo (widehat {OBH}). b) Bán kính R của đường tròn.
Đề bài
Cho hai điểm A, B trên đường tròn (O; R). Cho biết AB = 9 cm và khoảng cách từ O đến đường thẳng AB là OH = \(\frac{R}{2}\) . Tính:
a) Số đo \(\widehat {OBH}\) .
b) Bán kính R của đường tròn.
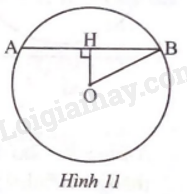
Phương pháp giải - Xem chi tiết
Dựa vào: Vận dụng tỉ số lượng giác của góc nhọn và hệ thức giữa cạnh và góc giúp giải tam giác vuông thuận lợi và nhanh chóng.
Lời giải chi tiết
a) Trong tam giác OHB vuông tại H, ta có \(\sin \widehat {OBH} = \frac{{OH}}{{OB}} = \frac{{\frac{R}{2}}}{R} = \frac{1}{2}\), suy ra \(\widehat {OBH} = {30^o}\).
b) Ta có OB = OA = R, suy ra tam giác AOB cân tại O, suy ra \(HB = HA = \frac{{AB}}{2} = \frac{9}{2} = 4,5(cm)\).
Trong tam giác OHB vuông tại H, ta có \(OB = \frac{{BH}}{{\cos \widehat {OBH}}} = \frac{{4,5}}{{\cos {{30}^o}}} = \frac{{4,5}}{{\frac{{\sqrt 3 }}{2}}} = 3\sqrt 3 (cm)\).
Suy ra R = OB = \(3\sqrt 3 (cm)\).