Giải bài 7 trang 57 sách bài tập toán 8 - Chân trời sáng tạo
Cho tứ giác ABCD có hai đường chéo vuông góc với nhau tại I. Cho biết (BC = 15cm,CD = 24cm) và (AD = 20cm.) Tính độ dài AB.
Đề bài
Cho tứ giác ABCD có hai đường chéo vuông góc với nhau tại I. Cho biết \(BC = 15cm,CD = 24cm\) và \(AD = 20cm.\) Tính độ dài AB.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về đường chéo của tứ giác: Trong tứ giác, đường chéo là đoạn thẳng nối hai đỉnh đối nhau.
+ Sử dụng kiến thức về định lí Pythagore vào tam giác vuông: Trong một tam giác vuông, bình vuông độ dài của cạnh huyền bằng tổng các bình phương độ dài của hai cạnh góc vuông.
Lời giải chi tiết
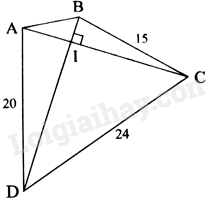
Áp dụng định lí Pythagore vào tam giác AIB vuông tại I ta có: \(I{A^2} + I{B^2} = A{B^2}\)
Áp dụng định lí Pythagore vào tam giác CIB vuông tại I ta có: \(I{C^2} + I{B^2} = B{C^2}\)
Áp dụng định lí Pythagore vào tam giác AID vuông tại I ta có: \(I{A^2} + I{D^2} = A{D^2}\)
Áp dụng định lí Pythagore vào tam giác CID vuông tại I ta có: \(I{C^2} + I{D^2} = C{D^2}\)
Do đó: \(A{B^2} + C{D^2} = \left( {I{A^2} + I{D^2}} \right) + \left( {I{C^2} + I{B^2}} \right)\)
\(A{B^2} + C{D^2} = A{D^2} + B{C^2}\)
\(A{B^2} = A{D^2} + B{C^2} - C{D^2} = {20^2} + {15^2} - {24^2} = 49\)
Do đó, \(AB = 7cm\)