Giải bài 7 trang 60 sách bài tập toán 8 - Chân trời sáng tạo tập 2
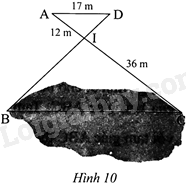
Người ta ứng dụng hai tam giác đồng dạng để đo khoảng cách BC ở hai điểm không đến được (Hình 10). Biết AD//BC.
Đề bài
Người ta ứng dụng hai tam giác đồng dạng để đo khoảng cách BC ở hai điểm không đến được (Hình 10). Biết AD//BC.
a) Chứng minh rằng $\Delta IDA\backsim \Delta IBC$
b) Tính khoảng cách BC.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về định lí về hai tam giác đồng dạng: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
+ Định lí trên cũng đúng trong trường hợp đường thẳng a cắt phần kéo dài hai cạnh của tam giác và song song với cạnh còn lại.
Lời giải chi tiết
a) Tam giác AID có: AD//BC nên $\Delta IDA\backsim \Delta IBC$
b) Vì nên \(\frac{{IA}}{{IC}} = \frac{{AD}}{{BC}}\) hay \(\frac{{12}}{{36}} = \frac{{17}}{{BC}}\). Vậy \(BC = \frac{{17.36}}{{12}} = 51\left( m \right)\)