Giải bài 7 trang 72 SGK Toán 8 – Chân trời sáng tạo
Mặt bên của một chiếc vali (Hình 17a) có dạng
Đề bài
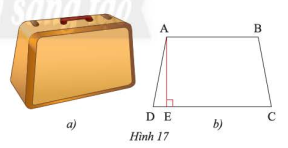
Mặt bên của một chiếc vali (Hình 17a) có dạng hình thang cân và được vẽ lại như Hình 17b. Biết hình thang đó có độ dài đường cao là \(60\) cm, cạnh bên là \(61\) cm và đáy lớn là \(92\) cm. Tính độ dài đáy nhỏ.
Phương pháp giải - Xem chi tiết
Tính \(DE\) (sử dụng định lý Pythagore)
Tính \(AB\)
Lời giải chi tiết
Áp dụng định lý Pythagore vào tam giác vuông \(ADE\) ta có:
\(D{E^2} + A{E^2} = A{D^2}\)
\(D{E^2} = A{D^2} - A{E^2} = {61^2} - {60^2} = 121 = {11^2}\)
\(DE = 11\) (cm)
Độ dài \(AB\) là: \(92 - 11.2 = 70\) (cm)
Cùng chủ đề:
Giải bài 7 trang 72 SGK Toán 8 – Chân trời sáng tạo