Giải bài 8 trang 92 vở thực hành Toán 8 tập 2
Cho tam giác ABC cân tại A và M là trung điểm của cạnh BC. Lấy các điểm D, E lần lượt trên các cạnh AB, AC sao cho $\widehat{DME}=\widehat{ABC}$.
Đề bài
Cho tam giác ABC cân tại A và M là trung điểm của cạnh BC. Lấy các điểm D, E lần lượt trên các cạnh AB, AC sao cho $\widehat{DME}=\widehat{ABC}$.
a) Chứng minh $\Delta BDM\backsim \Delta CME$.
b) Chứng minh DM là phân giác của góc BDE.
Phương pháp giải - Xem chi tiết
a) Chứng minh $\Delta BDM$ và $\Delta CME$ có hai cặp góc bằng nhau nên đồng dạng.
b) Chứng minh $\Delta MDE\backsim \Delta CME$ suy ra cặp góc $\widehat{BDM}=\widehat{MDE}$.
Lời giải chi tiết
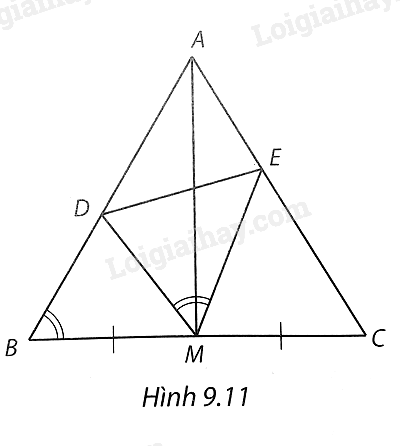
a) Xét hai tam giác BDM và CME, ta có:
\(\widehat{DBM}=\widehat{ABC}=\widehat{BCA}=\widehat{MCE}\),
$\widehat{BDM}={{180}^{0}}-\widehat{BMD}-\widehat{DBM}=\widehat{DMC}-\widehat{DME}=\widehat{EMC}$
Vậy $\Delta BDM\backsim \Delta CME$ (g.g)
b) Vì $\Delta BDM\backsim \Delta CME$ nên $\widehat{BDM}=\widehat{CME}$ và $\frac{DM}{ME}=\frac{BM}{CE}=\frac{MC}{CE}$, hay $\frac{DM}{MC}=\frac{ME}{CE}$.
Xét hai tam giác MDE và CME, ta có:
$\frac{DM}{MC}=\frac{ME}{CE}$ (theo chứng minh trên),
$\widehat{DME}=\widehat{ABC}=\widehat{BCA}=\widehat{MCE}$.
Vậy $\Delta MDE\backsim \Delta CME$ (c.g.c).
Suy ra $\widehat{MDE}=\widehat{CME}=\widehat{BDM}$, hay DM là phân giác của góc BDE.