Giải Bài 80 trang 92 sách bài tập toán 7 - Cánh diều — Không quảng cáo

Đề bài

Cho tam giác ABC có $\widehat {ABC} + \widehat {ACB} = 2\widehat {BAC}$ . Hai tia phân giác của góc B và góc C cắt nhau tại K. Trong các phát biểu sau, phát biểu nào sai ?

a) Số đo góc KAC bằng 30°.

b) Số đo góc BAK bằng 25°.

c) Số đo góc BKC bằng 120°.

d) Số đo góc BKC bằng 115°.

Lời giải chi tiết

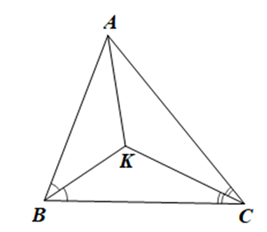
• Xét ∆ABC có $\widehat {ABC} + \widehat {ACB} + \widehat {BAC} = 180^\circ$ (tổng ba góc của một tam giác)

Mà $\widehat {ABC} + \widehat {ACB} = 2\widehat {BAC}$ nên $3\widehat {BAC} = 180^\circ$

Suy ra $\widehat {BAC} = \frac{{180^\circ }}{3} = 60^\circ$

Xét tam giác ABC có hai tia phân giác của góc B và góc C cắt nhau tại K

Nên AK là tia phân giác của góc BAC.

Suy ra $\widehat {KAB} = \widehat {KAC} = \frac{1}{2}\widehat {BAC} = \frac{{60^\circ }}{2} = 30^\circ$

Do đó phát biểu a là đúng, phát biểu b là sai.

•Vì BK là tia phân giác của góc ABC nên $\widehat {KBC} = \widehat {KBA} = \frac{1}{2}\widehat {ABC}$

Vì CK là tia phân giác của góc ACB nên $\widehat {KCB} = \widehat {KCA} = \frac{1}{2}\widehat {ACB}$

Suy ra $\widehat {KBC} + \widehat {KCB} = \frac{1}{2}\widehat {ABC} + \frac{1}{2}\widehat {ACB}$

Mà $\widehat {ABC} + \widehat {ACB} = 2\widehat {BAC} = 2.60^\circ  = 120^\circ$

Do đó $\widehat {KBC} + \widehat {KCB} = \frac{1}{2}\left( {\widehat {ABC} + \widehat {ACB}} \right) = \frac{{120^\circ }}{2} = 60^\circ$

Xét ∆KBC có $\widehat {KBC} + \widehat {KCB} + \widehat {CKB} = 180^\circ$ (tổng ba góc của một tam giác)

Nên $\widehat {CKB} = 180^\circ  - \left( {\widehat {KBC} + \widehat {KCB}} \right) = 180^\circ  - 60^\circ  = 120^\circ$.

Do đó phát biểu c là đúng, phát biểu d là sai.

Vậy phát biểu sai là b và d.