Giải Bài 82 trang 92 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC vuông tại C có ˆCAB=60°CAB^=60° , AE là tia phân giác của góc CAB (E ∈ BC). Gọi D là hình chiếu của B trên tia AE, K là hình chiếu của E trên AB. Chứng minh:
Đề bài
Cho tam giác ABC vuông tại C có ˆCAB=60°CAB^=60° , AE là tia phân giác của góc CAB (E ∈ BC). Gọi D là hình chiếu của B trên tia AE, K là hình chiếu của E trên AB. Chứng minh:
a) EB là tia phân giác của góc DEK, EK là tia phân giác của góc BEA;
b) EC = ED = EK.
Phương pháp giải - Xem chi tiết
- Chứng mính: \(\widehat {KEB} = \widehat {DEB}\) suy ra EB là tía phân giác của góc DEK, \(\widehat {KEA} = \widehat {KEB}\) suy ra EK là tia phân giác của góc BEA.
- Chứng minh: ∆ACE = ∆AKE (cạnh huyền – góc nhọn) suy ra CE = KE và chứng minh ∆EKB = ∆EDB (cạnh huyền – góc nhọn) suy ra EK = ED. Từ đó suy ra EC = ED = EK.
Lời giải chi tiết
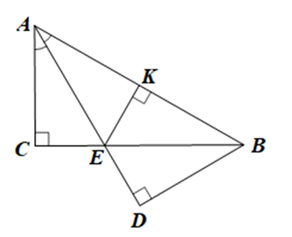
a) Tam giác ABC vuông tại C có \(\widehat {CAB} + \widehat {CBA} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Suy ra \(\widehat {CBA} = 90^\circ - \widehat {CAB} = 90^\circ - 60^\circ = 30^\circ \).
Tam giác EBK vuông tại K có (trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Suy ra \(\widehat {KEB} = 90^\circ - \widehat {KBE} = 90^\circ - 30^\circ = 60^\circ \).
•Vì AE là tia phân giác của góc CAB nên \(\widehat {CAE} = \widehat {BAE} = \frac{1}{2}\widehat {CAB} = \frac{1}{2}.60^\circ = 30^\circ \).
Tam giác ACE vuông tại C có \(\widehat {CEA} + \widehat {CAE} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Suy ra \(\widehat {CEA} = 90^\circ - \widehat {CAE} = 90^\circ - 30^\circ = 60^\circ \)
Do đó \(\widehat {DEB} = \widehat {CEA} = 60^\circ \) (hai góc đối đỉnh).
Ta có \(\widehat {KEB} = \widehat {DEB}\) (cùng bằng 60°) nên EB là tia phân giác của góc DEK.
•Ta có \(\widehat {KEA} + \widehat {KED} = 180^\circ \) (hai góc kề bù)
Hay \(\widehat {KEA} + \widehat {KEB} + \widehat {BED} = 180^\circ \)
Suy ra \(\widehat {KEA} = 180^\circ - \widehat {KEB} - \widehat {BED} = 180^\circ - 60^\circ - 60^\circ = 60^\circ \)
Do đó \(\widehat {KEA} = \widehat {KEB}\) (cùng bằng 60°).
Nên EK là tia phân giác của góc BEA.
Vậy EB là tia phân giác của góc DEK, EK là tia phân giác của góc BEA.
b) Xét ∆ACE và ∆AKE có:
\(\widehat {ACE} = \widehat {AKE}\left( { = 90^\circ } \right)\)
AE là cạnh chung,
\(\widehat {CAE} = \widehat {KAE}\) (chứng minh câu a).
Do đó ∆ACE = ∆AKE (cạnh huyền – góc nhọn).
Suy ra CE = KE (hai cạnh tương ứng) (1)
Xét ∆EKB và ∆EDB có:
\(\widehat {EKB} = \widehat {E{\rm{D}}B}\left( { = 90^\circ } \right)\)
BE là cạnh chung,
\(\widehat {KEB} = \widehat {DEB}\) (chứng minh câu a)
Do đó ∆EKB = ∆EDB (cạnh huyền – góc nhọn).
Suy ra KE = DE (hai cạnh tương ứng) (2)
Từ (1) và (2) ta có EC = EK = ED.
Vậy EC = ED = EK.