Giải Bài 83 trang 92 sách bài tập toán 7 - Cánh diều — Không quảng cáo

Đề bài

Cho hai đường thẳng song song a, b và một đường thẳng c (c cắt a tại E, c cắt b tại F). Hai tia phân giác của các góc aEF và bFE cắt nhau tại I. Gọi A, B lần lượt là hình chiếu của I trên các đường thẳng a và b ( Hình 52 ).

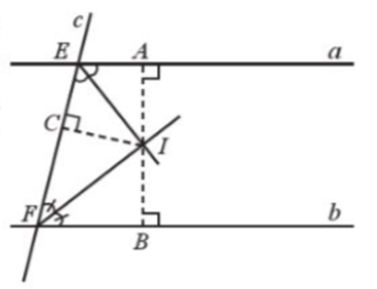
Chứng minh:

a) Tam giác EIF là tam giác vuông;

b) IA = IB.

Lời giải chi tiết

a) Vì EI là tia phân giác của góc aEF nên $\widehat {AEI} = \widehat {IEF} = \frac{1}{2}\widehat {AEF}$

Vì FI là tia phân giác của góc bFE nên $\widehat {BFI} = \widehat {IFE} = \frac{1}{2}\widehat {BFE}$.

Vì a // b nên $\widehat {aEF} + \widehat {bFE} = 180^\circ$ (hai góc trong cùng phía)

Suy ra $\widehat {IEF} + \widehat {IFE} = \frac{{\widehat {aEF} + \widehat {bFE}}}{2} = \frac{{180^\circ }}{2} = 90^\circ$.

Xét ∆IEF có  $\widehat {EIF} = 180^\circ  - \left( {\widehat {{\rm{IEF}}} + \widehat {IFE}} \right) = 180^\circ  - 90^\circ  = 90^\circ .$(tổng ba góc của một tam giác).

Suy ra

Vậy tam giác EIF là tam giác vuông tại I.

b) Gọi C là hình chiếu của I trên đường thẳng c.

Do EI là tia phân giác của góc AEF nên IA = IC (1)

Do FI là tia phân giác của góc EFB nên IC = IB (2)

Từ (1) và (2) ta có IA = IB.

Vậy IA = IB.