Giải Bài 78 trang 90 sách bài tập toán 7 - Cánh diều — Không quảng cáo

Đề bài

Cho tam giác DEF cân tại D có đường trung tuyến EM. Trên tia đối của tia ME lấy điểm N sao cho MN = ME.

a) Chứng minh DE = FN và tam giác DFN là tam giác cân.

b) Trên tia đối của tia FD lấy điểm A sao cho FA = FD. Chứng minh F là trọng tâm của tam giác NEA.

c) Chứng minh tam giác DNA là tam giác vuông.

d) Kẻ EB vuông góc với NA (B ∈ NA). Chứng minh ba điểm E, F, B thẳng hàng.

Lời giải chi tiết

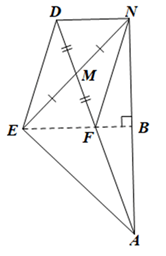
a) Xét ∆DME và ∆FMN có:

DM = FM (vì M là trung điểm của DF),

$\widehat {DME} = \widehat {FMN}$ (hai góc đối đỉnh),

ME = MN (giả thiết)

Do đó ∆DME = ∆FMN (c.g.c)

Suy ra DE = FN (hai cạnh tương ứng).

Vì tam giác DFE cân tại D nên DE = DF.

Do đó DE = DF = FN.

Tam giác DFN có DF = FN nên tam giác DFN cân tại F.

Vậy tam giác DFN cân tại F.

b) Ta có $M{\rm{D}} = MF = \frac{1}{2}DF$và FA = FD nên $MF = \frac{1}{2}F{\rm{A}}$

Mà AF + FM = AM nên AF + 1212AF = AM

Suy ra $\frac{2}{3}AF = AM$ hay $AF = \frac{2}{3}AM$.

Trong tam giác NEA có AM là trung tuyến và $AF = \frac{2}{3}AM$ nên F là trọng tâm của tam giác NEA.

Vậy F là trọng tâm của tam giác NEA.

c) • Ta có: DF = FN, DF = FA nên AF = FN.

Suy ra tam giác FNA cân tại F.

Do đó $\widehat {F{\rm{A}}N} = \widehat {FNA}$ (hai góc ở đáy)

•Vì tam giác DFN cân tại F nên $\widehat {FDN} = \widehat {FND}$ (hai góc ở đáy)

• Xét ∆DNA có $\widehat {A{\rm{D}}N} + \widehat {DNA} + \widehat {NAD} = 180^\circ$ (tổng ba góc của một tam giác)

Suy ra $\widehat {FND} + \widehat {DNA} + \widehat {FNA} = 180^\circ$

Hay $\left( {\widehat {FND} + \widehat {FNA}} \right) + \widehat {DNA} = \widehat {DNA} + \widehat {DNA} = 180^\circ$

Suy ra $2\widehat {DNA} = 180^\circ$

Do đó $\widehat {DNA} = \frac{{180^\circ }}{2} = 90^\circ$

Vậy tam giác DNA là tam giác vuông tại N.

d) Xét ∆DMN và ∆FME có:

DM = FM (vì M là trung điểm của DF),

$\widehat {DMN} = \widehat {FME}$ (hai góc đối đỉnh),

EM = MN (giả thiết)

Do đó ∆DMN = ∆FME (c.g.c)

Suy ra $\widehat {MDN} = \widehat {MFE}$ (hai góc tương ứng)

Mà hai góc này ở vị trí so le trong

Nên EF // DN

Lại có $\widehat {DNA} = 90^\circ$ (chứng minh câu c) hay DN ⊥ NA.

Suy ra EF ⊥ NA (một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại).

Mặt khác EB ⊥ NA (giả thiết)

Suy ra ba điểm E, F, B cùng nằm trên một đường thẳng.

Vậy ba điểm E, F, B thẳng hàng.