Giải Bài 77 trang 90 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC cân tại A có đường trung tuyến AD, G là trọng tâm. Trên tia đối của tia DA lấy điểm E sao cho DE = DG.
Đề bài
Cho tam giác ABC cân tại A có đường trung tuyến AD, G là trọng tâm. Trên tia đối của tia DA lấy điểm E sao cho DE = DG.
a) Chứng minh BG = GC = CE = BE.
b) Chứng minh ∆ABE = ∆ACE.
c) Nếu \(CG = \frac{1}{2}A{\rm{E}}\) thì tam giác ABC là tam giác gì? Vì sao?
Phương pháp giải - Xem chi tiết
- Chứng minh: GB = GC, EB = EC, BG = BE suy ra BG = GC = BE = CE.
- Chứng minh: \(\Delta ABE = \Delta AC{\rm{E}}(c - c - c)\)
- Nếu \(CG = \frac{1}{2}A{\rm{E}}\) thì chứng minh: tam giác ABC cân có \(\widehat {ACB} = {60^o}\) nên tam giác ABC là tam giác đều.
Lời giải chi tiết
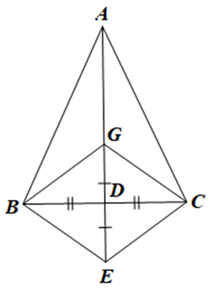
a) Xét tam giác ABC cân tại A nên AB = AC (hai cạnh bên).
Xét ∆ABD và ∆ACD có:
AB = AC (do ∆ABC cân tại A),
DB = DC (do D là trung điểm của BC),
AD là cạnh chung
Do đó ∆ABD = ∆ACD (c.c.c)
Suy ra \(\widehat {ADB} = \widehat {ADC}\) (hai góc tương ứng).
Mà \(\widehat {ADB} + \widehat {ADC} = 180^\circ \) (hai góc kề bù)
Nên \(\widehat {ADB} = \widehat {ADC} = \frac{{180^\circ }}{2} = 90^\circ \)
Suy ra AD vuông góc với BC.
Mặt khác D là trung điểm của BC
Do đó AD là đường trưng trực của đoạn thẳng BC.
Suy ra GB = GC (1)
Lại có điểm E nằm trên đường thẳng AD nên E cũng nằm trên đường trung trực của BC.
Do đó EB = EC (2)
Xét ∆BGD và ∆BED có:
\(\widehat {BDG} = \widehat {BDE}\left( { = 90^\circ } \right)\),
BG là cạnh chung,
DG = DE (giả thiết)
Do đó ∆BGD = ∆BED (hai cạnh góc vuông)
Suy ra BG = BE (3)
Từ (1), (2) và (3) suy ra BG = GC = CE = BE.
Vậy BG = GC = CE = BE.
b) Xét ∆ABE và ∆ACE có:
AB = AC (do ∆ABC cân tại A),
BE = CE (chứng minh câu a),
AE là cạnh chung
Do đó ∆ABE = ∆ACE (c.c.c).
Vậy ∆ABE = ∆ACE.
c) Ta có GD = ED (giả thiết) nên \(G{\rm{D}} = \frac{1}{2}GE\)
Mà G là trọng tâm của tam giác ABC nên \(G{\rm{D}} = \frac{1}{2}AG\).
Do đó AG = GE hay G là trung điểm của AE nên \(GE = \frac{1}{2}A{\rm{E}}\).
Mặt khác \(CG = \frac{1}{2}A{\rm{E}}\)
Suy ra GE = GC.
Theo câu a ta lại có GC = EC.
Khi đó GC = GE = EC.
+) Tam giác CGE có GC = GE = EB nên tam giác CGE là tam giác đều
Do đó \(\widehat {CGE} = 60^\circ \)
Suy ra:
• \(\widehat {CGD} + \widehat {GCD} = 90^\circ \) (tổng hai góc nhọn trong tam giác vuông CGD bằng 90°)
Suy ra \(\widehat {GCD} = 90^\circ - \widehat {CGD} = 90^\circ - 60^\circ = 30^\circ \)
• \(\widehat {CGE} + \widehat {AGC} = 180^\circ \) (hai góc kề bù)
Nên \(\widehat {AGC} = {180^o} - \widehat {CGE} = {180^o} - {60^o} = {120^o}\)
Mà GA = GC nên tam giác AGC cân tại G, do đó \(\widehat {GAC} = \widehat {GCA}\)
Lại có \(\widehat {GAC} + \widehat {GCA} + \widehat {AGC} = 180^\circ \) (tổng ba góc của tam giác AGC).
Do đó \(\widehat {GAC} = \widehat {GCA} = \frac{{180^\circ - \widehat {AGC}}}{2} = \frac{{180^\circ - 120^\circ }}{2} = 30^\circ \)
+) Ta có \(\widehat {ACB} = \widehat {ACG} + \widehat {GCB}\) (hai góc kề nhau)
Hay \(\widehat {ACB} = 30^\circ + 30^\circ = 60^\circ \)
Tam giác cân ABC có \(\widehat {ACB} = 60^\circ \) nên là tam giác đều.
Vậy tam giác ABC đều.