Giải Bài 9. 15 trang 55 sách bài tập toán 7 - Kết nối tri thức với cuộc sống — Không quảng cáo

Đề bài

Gọi M là trung điểm của cạnh BC của tam giác ABC và D là điểm sao cho M là trung điểm của AD. Đường thẳng qua D và trung điểm của AB cắt BC tại U, đường thẳng qua D và trung điểm của AC cắt BC tại V. Chứng minh BU = UV = VC.

Lời giải chi tiết

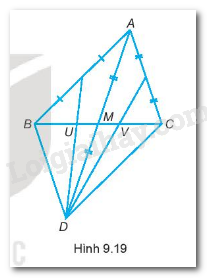
-Xét tam giác ABD có:

M là trung điểm của AD, DU đi qua trung điểm AB

=>BM và DU là 2 đường trung tuyến của tam giác

Mà BM cắt DU tại U

=>U là trọng tâm tam giác ABD.

$\Rightarrow BU = 2UM = \dfrac{2}{3}BM$(1)

-Xét tam giác ACD:

M là trung điểm của AD, DV đi qua trung điểm AC

=>CM và DV là 2 đường trung tuyến của tam giác

Mà CM cắt DV tại V

=>V là trọng tâm tam giác ACD.

$\Rightarrow CV = 2MV = \dfrac{2}{3}MC$(2)

Mà M là trung điểm BC

$\Rightarrow MB = MC$

Lại có: UV = UM + MV = $\dfrac{1}{3}BM + \dfrac{1}{3}CM = \dfrac{1}{3}BM + \dfrac{1}{3}BM = \dfrac{2}{3}BM$ (3)

Từ (1), (2) và (3) suy ra:

BU = UV = VC.