Giải bài 9.28 trang 57 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
Cho tam giác ABC và điểm D trên cạnh AC sao cho \(\widehat {ABD} = \widehat {BCA}.\) Chứng minh rằng: \(A{B^2} = AD.AC\)
Đề bài
Cho tam giác ABC và điểm D trên cạnh AC sao cho \(\widehat {ABD} = \widehat {BCA}.\) Chứng minh rằng: \(A{B^2} = AD.AC\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về định lý (trường hợp đồng dạng góc – góc): Nếu hai góc của tam giác lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết
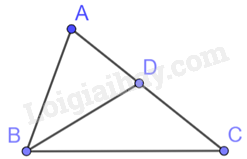
Tam giác ABD và tam giác ACB có:
\(\widehat A\;chung,\widehat {ABD} = \widehat {BCA}\left( {gt} \right)\)
Do đó, $\Delta ABD\backsim \Delta ACB\left( g-g \right)$
Suy ra: \(\frac{{AD}}{{AB}} = \frac{{AB}}{{AC}}\) nên \(A{B^2} = AD.AC\)
Cùng chủ đề:
Giải bài 9. 28 trang 57 sách bài tập toán 8 - Kết nối tri thức với cuộc sống