Giải bài 9.35 trang 59 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
Hãy tính độ dài các cạnh của một hình thoi với hai đường chéo lần lượt có độ dài bằng 6cm và 8cm.
Đề bài
Hãy tính độ dài các cạnh của một hình thoi với hai đường chéo lần lượt có độ dài bằng 6cm và 8cm.
Phương pháp giải - Xem chi tiết
+ Sử dụng tính của hình thoi để chỉ ra tam giác vuông và tính cạnh góc vuông: Trong hình thoi, hai đường chéo vuông góc với nhau tại trung điểm mỗi đường.
+ Sử dụng kiến thức định lí Pythagore để tính độ dài cạnh hình thoi: Trong một tam giác vuông, bình phương cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
Lời giải chi tiết
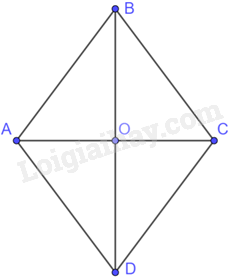
Giả sử hình thoi ABCD có hai đường chéo \(AC = 6cm,BD = 8cm\) và O là giao điểm của AC và BD. Khi đó, O là trung điểm của AC, O là trung điểm của BD và AC vuông góc với BD tại O.
Suy ra: \(OC = \frac{1}{2}AC = 3cm,OD = \frac{1}{2}BD = 4cm\)
\(\widehat {COD} = 90\)
Tam giác COD có: \(\widehat {COD} = 90\) nên tam giác COD vuông tại O. Theo định lí Pythagore ta có:
\(C{D^2} = O{C^2} + O{D^2} = {3^2} + {4^2} = 25\)
Suy ra \(CD = \sqrt {25} = 5cm\)