Giải bài tập 1. 2 trang 9 SGK Toán 12 tập 1 - Cùng khám phá — Không quảng cáo

Đề bài

a) $y =  - {x^3} + {x^2} - 5$

b) $y = \sqrt {{x^2} - x - 20}$

c) $y = {e^{{x^2}}}$

d) $y = \frac{x}{{{x^2} + 4}}$

Lời giải chi tiết

a) $y =  - {x^3} + {x^2} - 5$

Hàm số trên xác định trên R

Ta có : $y' =  - 3{x^2} + 2x$

Xét $y' =  - 3{x^2} + 2x = 0$$\Rightarrow \left[ \begin{array}{l}x = 0\\x = \frac{2}{3}\end{array} \right.$

Từ đó ta có bảng biến thiên :

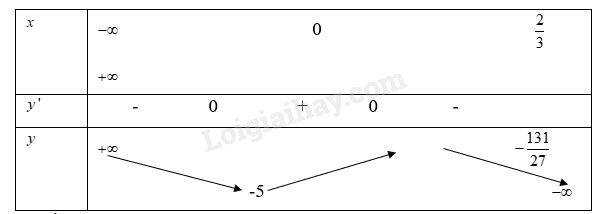
Từ bảng biến thiên ta có:

Hàm số đồng biến trên khoảng $\left( {0;\frac{2}{3}} \right)$

Hàm số nghịch biến trên khoảng $( - \infty ;0)$,$\left( {\frac{2}{3}; + \infty } \right)$

b) $y = \sqrt {{x^2} - x - 20}$

Hàm số trên xác định với ${x^2} - x - 20 \ge 0 \Rightarrow \left[ \begin{array}{l}x \ge 5\\x \le  - 4\end{array} \right.$

Ta có : $y' = \frac{{2x - 1}}{{2\sqrt {{x^2} - x - 20} }}$

Xét $y' = 0$$\Rightarrow 2x - 1 = 0$

$\Rightarrow x = \frac{1}{2}$

Từ đó ta có bảng biến thiên:

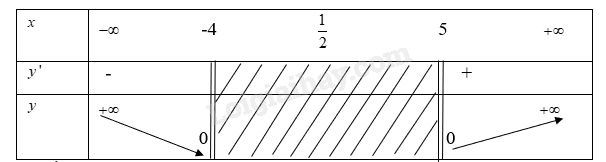
Từ bảng biến thiên ta có:

Hàm số đồng biến trên khoảng $(5; + \infty )$

Hàm số nghịch biến trên khoảng $( - \infty ; - 4)$

c) $y = {e^{{x^2}}}$

Hàm số trên xác định trên R

Ta có: $y' = {e^{{x^2}}}.2x$

Xét $y' = 0$$\Rightarrow x = 0$

Ta có bảng biến thiên

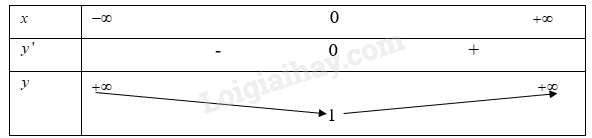
Từ bảng biến thiên ta có:

Hàm số trên nghịch biến trên khoảng$( - \infty ;0)$

Hàm số trên đồng biến trên khoảng$(0; + \infty )$

d) $y = \frac{x}{{{x^2} + 4}}$

Hàm số trên xác định trên R

Ta có: $y' = \frac{{{x^2} + 4 - x.2x}}{{{{({x^2} + 4)}^2}}}$

$= \frac{{ - {x^2} + 4}}{{{{({x^2} + 4)}^2}}}$

Xét $y' = 0$$\Rightarrow  - {x^2} + 4 = 0$$\Rightarrow \left[ \begin{array}{l}x = 2\\x =  - 2\end{array} \right.$

Ta có bảng biến thiên

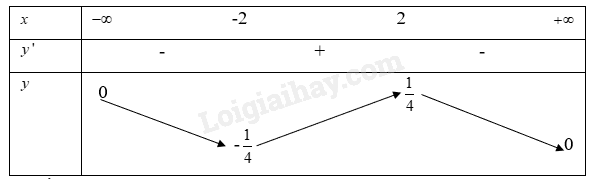
Từ bảng biến thiên ta có:

Hàm số trên nghịch biến trên khoảng $( - \infty ; - 2),(2; + \infty )$

Hàm số trên đồng biến trên khoảng $( - 2;2)$