Giải bài tập 1.5 trang 9 SGK Toán 12 tập 1 - Cùng khám phá
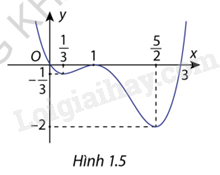
Cho hàm số \(y = f(x)\)liên tục trên đoạn \([0;3]\) thõa mãn \(f'\left( {\frac{1}{3}} \right) = f'(1) = f'\left( {\frac{5}{2}} \right) = 0\)và có đồ thị là đường cong như hình 1.5. Xác định các khoảng đơn điệu và tìm cực trị hàm số đã cho trên khoảng \((0;3)\)
Đề bài
Cho hàm số \(y = f(x)\)liên tục trên đoạn \([0;3]\) thõa mãn \(f'\left( {\frac{1}{3}} \right) = f'(1) = f'\left( {\frac{5}{2}} \right) = 0\)và có đồ thị là đường cong như hình 1.5. Xác định các khoảng đơn điệu và tìm cực trị hàm số đã cho trên khoảng \((0;3)\)
Phương pháp giải - Xem chi tiết
Từ những điều kiện bài cho lập bảng biến thiên rồi biện luận tính đơn điệu và cực trị hàm số
Lời giải chi tiết
Dựa vào dồ thị hàm số ta có:
Hàm số dồng biến trên khoảng \(\left( {\frac{1}{3};1} \right)\) và \(\left( {\frac{5}{2}; + \infty } \right)\)
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;\frac{1}{3}} \right)\) và \(\left( {1;\frac{5}{2}} \right)\)
Từ đồ thị hàm số ta lại có bảng biến thiên là:
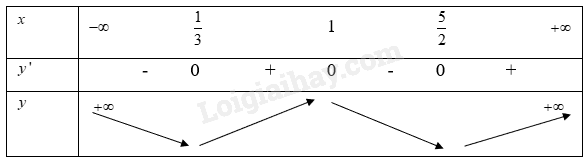
Từ bảng biến thiên ta có:
Hàm số đạt cực trị tại các điểm \(x = \frac{1}{3}\) , \(x = 1\) ,\(x = \frac{5}{2}\)