Giải bài tập 1.24 trang 32 SGK Toán 12 tập 1 - Kết nối tri thức
Một cốc chứa 30ml dung dịch KOH (potassium hydroxide) với nồng độ 100mg/ml. Một bình chứa dung dịch KOH khác chứa nồng độ 8mg/ml được trộn vào cốc. a) Tính nồng độ KOH trong cốc sau khi trộn x (ml) từ bình chứa, kí hiệu là C(x). b) Coi hàm C(x) là hàm số xác định với \(x \ge 0\). Khảo sát sự biến thiên và vẽ đồ thị của hàm số này. c) Giải thích tại sao nồng độ KOH trong cốc giảm theo x nhưng luôn lớn hơn 8mg/ml.
Đề bài
Một cốc chứa 30ml dung dịch KOH (potassium hydroxide) với nồng độ 100mg/ml. Một bình chứa dung dịch KOH khác chứa nồng độ 8mg/ml được trộn vào cốc.
a) Tính nồng độ KOH trong cốc sau khi trộn x (ml) từ bình chứa, kí hiệu là C(x).
b) Coi hàm C(x) là hàm số xác định với \(x \ge 0\). Khảo sát sự biến thiên và vẽ đồ thị của hàm số này.
c) Giải thích tại sao nồng độ KOH trong cốc giảm theo x nhưng luôn lớn hơn 8mg/ml.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về sơ đồ khảo sát hàm số phân thức để khảo sát và vẽ đồ thị hàm số:
Sơ đồ khảo sát hàm số phân thức
1. Tìm tập xác định của hàm số.
2. Khảo sát sự biến thiên của hàm số:
+ Tính đạo hàm y’. Tìm các điểm tại đó y’ bằng 0 hoặc đạo hàm không tồn tại.
+ Xét dấu y’ để chỉ ra các khoảng đơn điệu của hàm số.
+ Tìm cực trị của hàm số.
+ Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm tiệm cận của đồ thị hàm số.
+ Lập bảng biến thiên của hàm số.
3. Vẽ đồ thị của hàm số dựa vào bảng biến thiên.
Lời giải chi tiết
a) Khối lượng dung dịch trong cốc sau khi trộn x(ml) KOH từ bình chứa là: \(m = 30.100 + 8x = 8x + 3\;000\left( {mg} \right)\)
Thể tích dung dịch trong cốc sau khi trộn x(ml) KOH từ bình chứa là: \(V = 30 + x\left( {ml} \right)\)
Nồng độ KOH trong cốc sau khi trộn x (ml) từ bình chứa là:
\(C\left( x \right) = \frac{m}{V} = \frac{{8x + 3000}}{{30 + x}}\left( {mg/ml} \right)\)
b) Khảo sát hàm số \(y = C\left( x \right) = \frac{{8x + 3000}}{{x + 30}}\) với \(x \ge 0\).
1. Tập xác định của hàm số: \(\left[ {0; + \infty } \right)\)
2. Sự biến thiên:
\(C'\left( x \right) = \frac{{ - 2760}}{{{{\left( {x + 30} \right)}^2}}} < 0\forall x \ge 0\)
Hàm số nghịch biến trên \(\left( {0; + \infty } \right)\).
Hàm số không có cực trị.
\(\mathop {\lim }\limits_{x \to + \infty } C\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{8x + 3000}}{{x + 30}} = 8\).
Do đó, đồ thị hàm số \(y = C\left( x \right) = \frac{{8x + 3000}}{{x + 30}}\) nhận đường thẳng \(y = 8\) làm tiệm cận ngang (phần bên phải trục Oy)
Bảng biến thiên:

3. Đồ thị: Giao điểm của đồ thị hàm số với trục tung là (0;100).
Đồ thị hàm số \(y = C\left( x \right) = \frac{{8x + 3000}}{{x + 30}}\) đi qua các điểm (200; 20); \(\left( {120;\frac{{132}}{5}} \right)\).
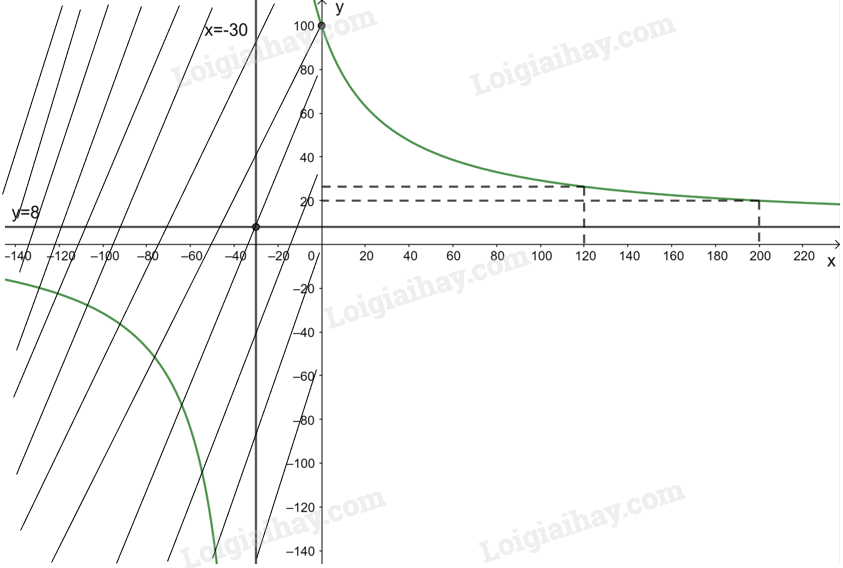
Đồ thị của hàm số \(y = C\left( x \right) = \frac{{8x + 3000}}{{x + 30}}\) với \(x \ge 0\) là phần nét màu xanh không bị gạch chéo.
c) Vì \(C'\left( x \right) = \frac{{ - 2760}}{{{{\left( {x + 30} \right)}^2}}} < 0\forall x \ge 0\) và \(\mathop {\lim }\limits_{x \to + \infty } C\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{8x + 3000}}{{x + 30}} = 8\) nên nồng độ KOH trong cốc giảm theo x nhưng luôn lớn hơn 8mg/ml