Giải bài tập 1 trang 89 SGK Toán 9 tập 2 - Cánh diều
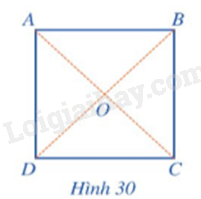
Cho hình vuông ABCD tâm O (Hình 30). Phép quay thuận chiều tâm O biến điểm A thành điểm D thì các điểm B, C, D tương ứng biến thành các điểm nào?
Đề bài
Cho hình vuông ABCD tâm O (Hình 30). Phép quay thuận chiều tâm O biến điểm A thành điểm D thì các điểm B, C, D tương ứng biến thành các điểm nào?
Phương pháp giải - Xem chi tiết
Xác định \(a^\circ \) trong “Phép quay thuận chiều \(a^\circ \) tâm O biến điểm A thành điểm D”.
Các trường hợp còn lại tương tự.
Lời giải chi tiết
Vì \( ABCD \) là hình vuông nên \( AC = BD \);
\( AC \perp BD \) tại \( O \), \( O \) là trung điểm của \( AC \), \( BD \).
Do đó \( {OA} = {OB} = {OB} = {OD} \) và
\( \widehat{AOB} = \widehat{BOC} = \widehat{COD} = \widehat{DOA} = 90^\circ \).
Ta có góc tạo bởi tia \( OA \) đến tia \( OD \) theo chiều quay của kim đồng hồ là:
\( \widehat{AOB} + \widehat{BOC} + \widehat{COD} = 270^\circ \).
Như vậy, phép quay thuận chiều \( 270^\circ \) tứ giác \( ABCD \) sẽ biến điểm \( A \) thành điểm \( D \), biến các điểm \( B, C, D \) thành các điểm \( A, B, C \).