Giải bài tập 10. 16 trang 107 SGK Toán 9 tập 2 - Kết nối tri thức — Không quảng cáo

Đề bài

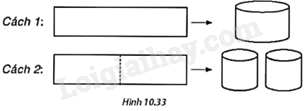
Từ một tấm tôn hình chữ nhật có kích thước \(50cm \times 240cm\), người ta làm mặt xung quanh của các thùng đựng nước hình trụ có chiều cao bằng 50cm, theo hai cách sau (H.10.33):

• Cách 1 : Gò tấm tôn ban đầu thành mặt xung quanh của thùng nước hình trụ.
• Cách 2 : Cắt tấm tôn ban đầu thành hai tấm bằng nhau hình chữ nhật, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.

Kí hiệu \({V_1}\) là thể tích của thùng gò được theo Cách 1 và \({V_2}\) là tổng thể tích của hai thùng gò được theo Cách 2 . Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\) (giả sử các mối hàn là không đáng kể).

Lời giải chi tiết

Theo cách 1, chu vi đường tròn đáy bằng 240cm nên \(2\pi R = 240\), suy ra \(R = \frac{{120}}{\pi }cm\).

Thể tích hình trụ là:

\({V_1} = \pi .{\left( {\frac{{120}}{\pi }} \right)^2}.50 = \frac{{720\;000}}{\pi }\left( {c{m^3}} \right)\)

Theo cách 2, chu vi 1 đường tròn đáy bằng 120cm nên \(2\pi {R_1} = 120\), suy ra \({R_1} = \frac{{60}}{\pi }cm\)

Tổng thể tích hai hình trụ gò được là:

\({V_2} = 2.\pi .{\left( {\frac{{60}}{\pi }} \right)^2}.50 = \frac{{360\;000}}{\pi }\left( {c{m^3}} \right)\)

Do đó, \(\frac{{{V_1}}}{{{V_2}}} = \frac{{\frac{{720\;000}}{\pi }}}{{\frac{{360\;000}}{\pi }}} = 2\).