Giải bài tập 10.26 trang 109 SGK Toán 9 tập 2 - Kết nối tri thức
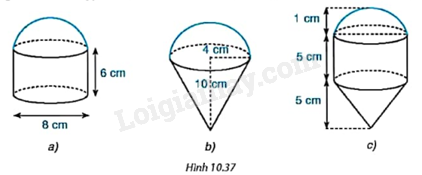
Các hình dưới đây (H.10.37) được tạo thành từ các nửa hình cầu, hình trụ và hình nón (có cùng bán kính đáy). Tính thể tích của các hình đó theo kích thước đã cho.
Đề bài
Các hình dưới đây (H.10.37) được tạo thành từ các nửa hình cầu, hình trụ và hình nón (có cùng bán kính đáy). Tính thể tích của các hình đó theo kích thước đã cho.
Phương pháp giải - Xem chi tiết
Thể tích hình a bằng tổng thể tích của hình trụ có đường kính đáy 8cm, chiều cao 6cm và nửa hình cầu có đường kính 8cm.
Thể tích hình b bằng tổng thể tích của hình nón có bán kính đáy 4cm, chiều cao 10cm và nửa hình cầu có bán kính 4cm.
Thể tích hình c bằng tổng thể tích của hình trụ có bán kính đáy 1cm, chiều cao 5cm, hình nón bán kính đáy 1cm, chiều cao 5cm và nửa hình cầu bán kính 1cm.
Lời giải chi tiết
Hình a: Bán kính đường tròn đáy là: \(R = \frac{8}{2} = 4cm\).
Thể tích của hình trụ có bán kính 4cm, chiều cao 6cm là:
\({V_1} = \pi {.4^2}.6 = 96\pi \left( {c{m^3}} \right)\).
Thể tích nửa hình cầu có bán kính 4cm là:
\({V_2} = \frac{1}{2}.\frac{4}{3}\pi {.4^3} = \frac{{128}}{3}\pi \left( {c{m^3}} \right)\).
Thể tích hình a là:
\(V = {V_1} + {V_2} = 96\pi + \frac{{128\pi }}{3} = \frac{{416\pi }}{3}\left( {c{m^3}} \right)\).
Hình b: Thể tích của hình nón có bán kính đáy 4cm, chiều cao 10cm là:
\({V_1} = \frac{1}{3}\pi {.4^2}.10 = \frac{{160\pi }}{3}\left( {c{m^3}} \right)\).
Thể tích nửa hình cầu có bán kính 4cm là:
\({V_2} = \frac{1}{2}.\frac{4}{3}\pi {.4^3} = \frac{{128\pi }}{3}\left( {c{m^3}} \right)\).
Thể tích hình b là:
\(V = {V_1} + {V_2} = \frac{{160\pi }}{3} + \frac{{128\pi }}{3} = 96\pi \left( {c{m^3}} \right)\).
Hình c: Thể tích của hình trụ có bán kính đáy 1cm, chiều cao 5cm là:
\({V_1} = \pi {.1^2}.5 = 5\pi \left( {c{m^3}} \right)\).
Thể tích của hình nón có bán kính đáy 1cm, chiều cao 5cm là:
\({V_2} = \frac{1}{3}\pi {.1^2}.5 = \frac{{5\pi }}{3}\left( {c{m^3}} \right)\).
Thể tích nửa hình cầu có bán kính 1cm là:
\({V_3} = \frac{1}{2}.\frac{4}{3}\pi {.1^3} = \frac{{2\pi }}{3}\left( {c{m^3}} \right)\).
Thể tích hình c là:
\(V = {V_1} + {V_2} + {V_3} = 5\pi + \frac{{5\pi }}{3} + \frac{{2\pi }}{3} = \frac{{22\pi }}{3}\left( {c{m^3}} \right)\).